介紹
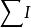節點電流定律 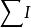節點電流定律在任一時刻，對電路中的任一節點，流入節點的電流之和等於流出節點的電流之和。即=。
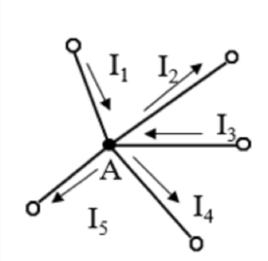
如圖，
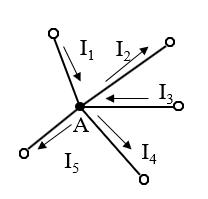節點電流定律
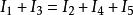節點電流定律對於節點A：。
節點電流定律移項有：。
如果規定流入節點的電流為正，流出節點的電流為負，則可得出下面的結論：
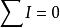節點電流定律電流定律第二種描述：
在任一電路的任一節點上，電流的代數和永遠等於零。
背景
節點電流定律這一難題，早在1847年，就被21歲的基爾霍夫(德國科學家)成功地解決了。
當時他剛從大學畢業，第一篇論文就提出後來被稱為基爾霍夫電流定律和電壓定律的兩個定律，運用這兩個定律能正確而迅速地求解任何複雜的電路，立即被各國科學家接受和採用，直到現在它仍是解決複雜電路問題的重要工具。基爾霍夫被稱為“電路求解大師”。
複雜電路概念
支路
有一個或幾個元件首尾相接構成無分支電路。
節點電流定律圖中有3條支路：
E1和R1串聯構成一條支路；
E2和R2串聯構成一條支路；
R3單獨構成另一條支路。
節點
三條或三條以上支路的連線點叫節點。
圖中A和B為節點。
迴路
電路中任一閉合路徑稱為迴路。
圖中共有3個迴路，分別是：
（1）A B D M A
（2）A N C B A
（3）M N C D M
網孔
內部不含有支路的迴路叫網孔。
步驟
①假設電流的參考方向
②確定節點
③列節點電流方程（列方程時，說明對哪一個節點套用定律）
④解方程，求出未知電流的大小與方向（若電流出現負值，必須用文字加以說明負號的含義。）
推廣
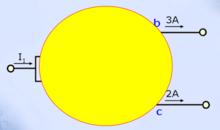
對於電路中任意假設的封閉面來說，節電流定律仍然成立。
節點電流定律把封閉面看成一個大節點
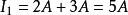節點電流定律推論
1、對於兩個網路如果有兩根導線相連，則兩 根導線中的電流必相等。
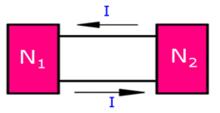節點電流定律2、若兩個網路之間只有一根導線相連，那么這根導線中一定沒有電流通過。 I = 0
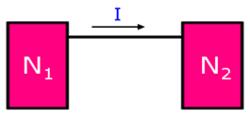節點電流定律3、若一個電路中只有一處用導線接地，則該接地線中沒有電流。I =0
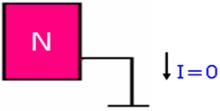節點電流定律注意事項
(1) 對於含有 n個節點的電路，只能列出( n- 1)個獨立的電流方程。
(2) 列節點電流方程時，只需考慮電流的參考方向，然後再帶入電流的數值。
為分析電路的方便，通常需要在所研究的一段電路中事先選定(即假定)電流流動的方向，叫做電流的參考方向，通常用“→”號表示。
電流的實際方向可根據數值的正、負來判斷，當 I > 0時，表明電流的實際方向與所標定的參考方向一致；當 I< 0時，則表明電流的實際方向與所標定的參考方向相反。
