定義
在下圖所示線性、無源n連線埠網路中：
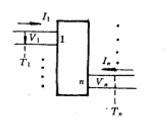節點阻抗矩陣用電流作自變數,可寫出其阻抗參量方程為：
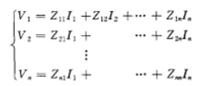節點阻抗矩陣將上述方程寫成矩陣形式為：【V】=【Z】【I】，其中【V】和【I】分別為多連線埠網路的電壓和電流列矩陣，而【Z】就是多連線埠網路的阻抗矩陣 。
相關導納矩陣
與阻抗矩陣相關的導納矩陣
若以電壓作為自變數，根據上述方程同樣可寫出導納參量方程及導納矩陣【Y】，在同一個多連線埠網路中，阻抗矩陣和導納矩陣互為逆矩陣。
矩陣特性
1.若多連線埠網路內部無各向異性質，則網路具有互異性，阻抗矩陣的轉置不變，即;
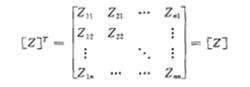節點阻抗矩陣2.當網路內無損耗時，則所有的阻抗矩陣參量均為純虛數。當網路無耗時，構成網路的均為電抗元件，則自阻抗或轉移阻抗 也是純電抗，因為它們都分別由網路內的電抗經串並聯後得到。
相關推論
由以上性質可知，對於互易的雙連線埠網路，只有三個獨立參量，如果網路又具有對稱性時，則只有二個獨立參量。因此在求矩陣元素時，可利用此性質加以簡化。
歸一化方法
歸一化阻抗矩陣
在微波工程中，一般均以特性阻抗的相對值來判別電路匹配的程度。這樣得出的矩陣參量稱歸一化參量，由此所得的矩陣，稱歸一化矩陣。為此，應首先將各連線埠的電壓、電流變換成歸一化量。仍以雙連線埠網路為例，若其二連線埠傳輸線的特性阻抗分別為Zc1和Zc2時，則歸一化電壓、電流按下式定義：
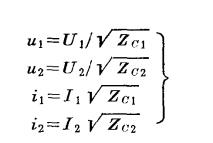節點阻抗矩陣其中小寫的符號均表示歸一化量。這樣則有：
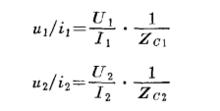節點阻抗矩陣從而得到了阻抗的歸一化。把歸一化的電壓寫成歸一化電流的表示式，由此得到的阻抗矩陣就為歸一化阻抗矩陣：
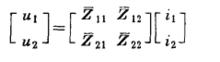節點阻抗矩陣存在缺點
（1）如果系統的自由度n比較大，則利用阻抗矩陣計算和實測的工作量比較大。
（2）如果只要求某幾個頻響函式的數值，用阻抗矩陣求解，則效率不高。
