概念簡介
等速萬向節的作用是將軸間有夾角或相互位置有變化的兩轉軸連線起來，並使兩軸以相同的角速度傳遞動力，它可以克服普通十字軸式萬向節存在的不等速性問題，特別適合於轉向驅動橋的使用。
轉向驅動橋中，前輪既是驅動輪，又是轉向輪，轉向時偏轉角度很大，最大可達40°以上，這時就不能採用傳統的、偏轉角度很小的普通萬向節了。普通萬向節在偏轉角較大時，轉速和扭矩會有很大的波動，汽車發動機的動力很難平穩可靠地傳輸給車輪，同時也會造成汽車的振動、衝擊和噪聲。因此，必須採用偏轉角度大、動力傳輸平穩、角速度均勻的等速萬向節才能滿足要求。
分類與結構
目前廣泛採用的等速萬向節主要有球叉式萬向節和球籠式萬向節，其中球叉式萬向節按照鋼球滾道形狀的不同，球叉式萬向節可分為圓弧滾道型和直槽滾道型兩種；按照萬向節軸向能否運動，球籠式萬向節分為固定型球籠式萬向節（RF節）和伸縮型球籠式萬向節（VL節）。
圓弧滾道型球叉式萬向節
圓弧滾道型球叉式萬向節的構造如下圖所示。主動叉與從動叉分別與內、外半軸製成一體。在主、從動叉上，各有4個曲面凹槽，裝合後形成兩個相交的環形槽作為鋼球滾道。4個傳動鋼球放在槽中，中心鋼球放在兩叉中心的凹槽內，以定中心。
為順利地將鋼球裝入槽內，在中心鋼球上銑出一個凹面，凹面中央有一深孔。裝合時，先將定位銷裝入從動叉內，放人中心鋼球，然後在兩球叉槽中陸續裝入3個傳動鋼球，再將中心鋼球的凹面對向未放鋼球的凹槽，以便裝入第4個傳動鋼球，而後再將中心鋼球的孔對準從動叉孔，提起從動叉軸使定位銷插進球孔中，最後將鎖止銷插入從動叉上與定位銷垂直的孔中，以限制定位銷軸向移動，保證中心鋼球的正確位置。
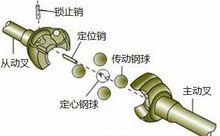圖1 圓弧滾道型球叉式萬向節球叉式萬向節結構簡單，允許最大夾角為32°～33°，一般套用於轉向驅動橋中；球叉式萬向節工作時，只有兩個鋼球傳力，反轉時，則由另兩個鋼球傳力。因此，鋼球與曲面凹槽之間的單位壓力較大，磨損較快，影響使用壽命。近年來，有些球叉式萬向節中省去了定位銷和鎖止銷，中心鋼球上也沒有凹面，靠壓力裝配。這樣，結構更為簡單，但是拆卸不便。
直槽滾道型球叉式萬向節
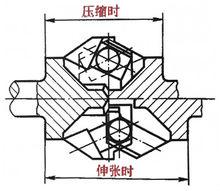圖2 直槽滾道型球叉式萬向節直槽滾道型球叉式萬向節的構造如下圖所示。兩個球叉上的直槽與軸的中心線傾斜相同的角度，彼此對稱。在兩球叉間的槽中裝有四個鋼球。由於兩球叉中的槽所處的位置是對稱的，這便保證了四個鋼球的中心處於兩軸夾角的平分面上。這種萬向節加工比較容易，允許的軸間夾角不超過20°，在兩叉間允許有一定量的軸間滑動。直槽滾道型球叉式萬向節主要套用於斷開式驅動橋中，當半軸擺動時，用它可以補償半軸的長度變化而省去滑動花鍵。
固定型球籠式萬向節（RF節）
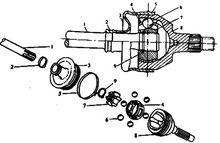圖3 固定型球籠式萬向節固定型球籠式萬向節的結構如下圖所示。星形套7以內花鍵與主動軸1相連，其外表面有6條凹槽，形成內滾道。球形殼8的內表面有相應的6條凹槽，形成外滾道，6個傳力鋼球分別裝在各條凹槽中，並由保持架4使之保持在一個平面內，動力有主動軸經傳力鋼球、球形殼輸出。
球籠式萬向節在兩軸最大夾角達到47°的情況下，仍可傳遞轉矩，且工作時，無論運動方向如何，6個鋼球全部傳力，與球叉式萬向節相比，其承載能力強，結構緊湊，拆裝方便，因此套用越來越廣泛。
伸縮型球籠式萬向節（VL節）
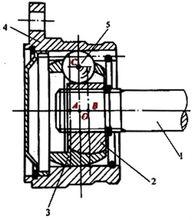圖4 伸縮型球籠式萬向節伸縮型球籠式萬向節的結構如下圖所示。該結構形式的內、外滾道是圓筒形的，在傳遞轉矩過程中，星形套2與筒形殼4可以沿軸向相對移動，故可省去其他萬向傳動裝置中必須有的滑動花鍵。這不僅使結構簡化，而且由於星形套2與筒形殼4之間的軸向相對移動是通過鋼球5沿內、外滾道滾動來實現的，與滑動花鍵相比，其滑動阻力小，最適用於斷開式驅動橋。這種萬向節保持架的內球面中心B與外球面中心A位於萬向節中心。的兩邊，且與O等距離。鋼球中心C到A、B距離相等，以保證萬向節作等角速傳動。
原理
等速萬向節的基本原理
在機械傳動中，解決有軸間夾角的等速動力傳遞，典型的例子是錐齒輪傳動。如下圖所示，一對大小相同的錐齒輪傳動，兩齒輪軸線夾角為a，兩齒輪的嚙合點P位於交角的平分面上，由P點分別到兩軸的垂直距離都等於r。在P點處兩齒輪的圓周速度是相等的，因而兩個齒輪旋轉的角速度也相等。從這個原理出發，若萬向節的傳力點在其夾角變化時始終位於角平分面內，則可使兩萬向節叉保持等角速傳動的關係。
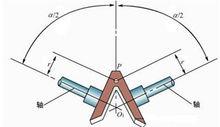圖5 等速萬向節的基本原理等速萬向節的基本原理就是從結構上保證萬向節在工作過程中，其傳力點始終位於主從動軸夾角的平分面上。
球叉式萬向節等角速傳動原理
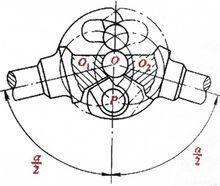圖6 球叉式萬向節等角速傳動原理可按下圖來說明球叉式萬向節的等角速傳動原理：主動叉和從動叉凹槽的中心線是以O1、O2為圓心的兩個半徑相等的圓，而圓心O1、O2與萬向節中心O的距離相等。因此，在主動軸和從動軸以任何角度相交的情況下，傳動鋼球中心都位於兩圓的交點上，亦即所有傳動鋼球都位於角平分面上，因而保證了等角速傳動。
球籠式萬向節等角速傳動原理
可按下圖來說明球籠式萬向節的等角速傳動原理：外滾道的中心A與內滾道的中心B分別位於萬向節中心O的兩邊，且與O等距離，有OA=OB。鋼球中心C到A、B兩點的距離也相等，有CA=CB，即傳力鋼球到主動軸和從動軸的距離a和b相等。在三角形△COA與△COB中，CO是共邊，有三角形△COA與△COB全等。由於保持架的
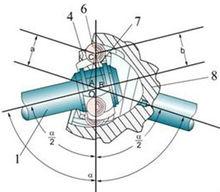圖7 球籠式萬向節等角速傳動原理內外球面、星形套的外球面和球形殼的內球面，均以萬向節中心O為球心，當兩軸夾角變化時，保持架可沿內、外球面滑動，以保持鋼球在一定位置。當兩軸相交任意角時，總有∠COA=∠COB成立，因此，傳力鋼球的中心C總是位於兩軸夾角的平分面上，保證了從動軸與主動軸等角速轉動。
