定律簡述
 第一數字定律
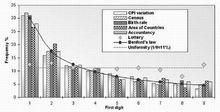
第一數字定律(圖)本圖表中的幾個數據範例來自於西班牙國家統計局,數據是按照本福特對數定律統計的。然而,按照彩票獲得的數據是隨機的和統一的。
定律統計
您住宅地址號碼是以a 1開始的嗎?根據一個奇特的數學定律統計,約三分之一的住宅號碼是以1作為其首個數字的。其它許多幾乎沒有任何共通性的地區也有相同的情況:比如道瓊斯指數的歷史數據、個人電腦中檔案儲存的大小排列順序、世界主要河流的長度、報紙頭版頭條的數字及其它許多事情。
定律發現
該定律根據其第二位奠基人弗蘭克.本福特的名字被命名為本福特定律。通用電氣公司物理學家本福特於1935年發現了這一定律。該定律告訴人們在各種各樣不同資料庫中每個數字(從1到9)作為首個重要阿拉伯數字的頻率。
除數字1始終占據約三分之一的出現頻率外,數字2的出現頻率為17.6%,3出現的頻率為12.5%,依次遞減,9的出現頻率是4.6%。在數學術語中,這一對數定律的公式為F(d) = log[1 + (1/d)],此公式中F代表頻率,D代表待求證數字。
這一現象讓人覺得很奇怪,來自科爾多瓦大學的科學家傑赫斯.托里斯、桑索利斯.費爾羅德滋、安東尼奧.迦米洛和安東尼奧.索拉同樣也如此認為。科學家們在《歐洲物理雜誌》上發表了一篇題為“數字如何開始?(第一數字定律)”的文章,該文章對這一定律進行了簡要的歷史回顧。他們的論文同時還對第一數字定律的有效套用進行了闡述,並對為何沒有人能夠對這一數字出現頻率現象做出合理解釋的原因進行了闡述。
電漿物理學專家托里斯說,“自從我了解本福特定律以來,它一直是我很感興趣的問題之一。在統計物理學課堂上,我一直將此定律作為一個令人驚奇的範例來激發學生們的好奇心。”托里斯解釋道,在本福特之前,有一位深受尊敬的天文學家名為西蒙.紐庫姆,他在1881年發現了這一定律。紐庫姆同時代的科學家們並沒有對他的科學發現引起足夠重視。本福特和紐庫姆兩位科學家均對這一定律感到困惑:當瀏覽對數表書籍時,他們注意到書的開始部分要比結束部分髒得多。這就是說他們的同事到圖書館後,選擇各種各樣學科書籍時首選第一頁開始閱讀。
深入研究
本福特對此疑問的觀察要比紐庫姆更深入一些。他開始對其它數字進行調查,發現各個完全不相同的數據,比如人口、死亡率、物理和化學常數、棒球統計表、半衰期放射性同位數、物理書中的答案、素數數字和斐波納契數列數字中均有“第一數字定律”現象的出現。換句話說就是只要是由度量單位制獲得的數據都符合這一定律。
不符特例
另一方面,任意獲得的和受限數據通常都不符合本福特定律。比如,彩票數字、電話號碼、汽油價格、日期和一組人的體重或者身高數據是比較隨意的,或者是任意指定的,並不是由度量單位制獲得的。
正如托里斯和他的同事所解釋的,數十年來科學家緊隨本福特對這一數字現象進行研究,但是除了發現更多的例子外,他們幾乎沒有發現有關比第一數字定律本身更多的東西。然而科學家們還是發現一些奇特現象。比如當對資料庫中的第二重要數字進行調查時,該定律仍然發揮著作用,但是第二重要數字的重要性卻降低。同樣,第三和第四重要數字所展現出來的特徵就開始變得相同起來,第五重要數字的頻率為10%,剛好是平均數。第二個奇特現象引發了更多的科學興趣:
科學家們在他們所發表的文章中寫到,“1961年,皮克漢姆發現了首個常規相關結論,該結論顯示本福特定律是一個尺度不變原理,同時也是唯一一個提出數字尺度不變原理的定律。那就是說,由於是以公里來表示世界河流的長度,因此它滿足本福特定律,同樣以英里、光年、微米或者其它長度單位數字都會滿足這一定律。”
其他說明
托里斯同時還解釋到,在二十世紀晚期,一些重要的預測理論(基數恆定性及唯一性等)被特德.希爾和其它數學家證實。雖然一些範例(比如住宅地址號幾乎總是以數字1開頭,低位數總是出現在高位數之前)得到了解釋,但是目前仍然沒有找到任何能解釋各種範例的能用判斷標準。科學家們同時還解釋到,沒有任何優先標準能夠告訴我們什麼時候應當或者不應當遵守這一定律設定數字。托里斯說,“現在對該定律的研究取得了許多理論成果,但是一些理論成果仍然是前途未明。為什麼一些數字設定,比如通用物理學恆量會如此完美地符合這一定律?我們不僅要了解這一定律的數學原因,還要掌握這一套實驗數據的特徵。比如他們的連線點是什麼?他們來自哪裡?很顯然,他們是相當獨立的。我希望將來能夠找到這一定律的總體必然性和充分條件。很多人都對這一定律感興趣,特別是經濟學家。但是我也知道這一定律也許有可能是永遠都不可能的事。”
實踐套用
然而,科學家們已經使用該定律進行了許多實踐套用。比如,一個公司的年度賬目數據應當是滿足這一定律,經濟學家可以根據這一定律查找出偽造數據。因為偽造數據很難滿足這一定律。(非常有趣的是,科學家發現數字5和6,而不是1是最流行的數字,這表明偽造者試圖在賬目中間“隱藏”數據。)
本福特定律最近還用於選舉投票欺詐發現。科學家依據這一定律發現了2004年美國總統選舉中佛羅里達州的投票欺詐行為,2004年委內瑞拉的投票欺詐和2006年墨西哥投票欺詐。
托里斯說,“有關第一數字定律是通過髒書頁發現的故事是完全不可信的。本福特定律不可否認已經得到套用。當這一定律被發現是其能夠帶來的好處並不明朗。對我而言,它仿佛僅僅只是一個數字奇異現象。這就是簡單中可能蘊涵有意想不到神奇之處的典型範例。”
