概念
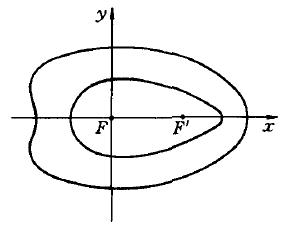 圖1
圖1給定兩定點F 、F',假定P點與F、F'的距離分別為r1與r2, 若滿足方程:m*r1+n*r2=d,其中,m、n、d都是常數,則稱P點的軌跡為笛卡爾卵形線。當m=n時,為橢圓。在一般情況下,笛卡兒卵形線是四次曲線,它包括兩個沒有共同點的閉曲線,而且一個在另一個之內。在內的一個類似於橢圓,在外的一個可能是凸的,也可能有拐點(如圖1所示)。
光學性質
笛卡兒(Descartes , R. )在《折光》里討論了這個曲線和它的折光性質,他成功地解決了什麼樣的曲面作為兩種介質的交界面時,能使從第一種介質內一點發出的光線射到曲面上,折入第二種介質而聚於一點。他發現具有這個性質的旋轉面是由笛卡兒卵形線產生的。
選取適當的m、n值,可使通過點A的光線經折射後,全部通過點B。笛卡爾曾利用這個光學性質,選取笛卡兒卵形線作為透鏡的截面形狀,用來消除球面像差。
卡西尼卵形線
 笛卡兒卵形線
笛卡兒卵形線設A,B是平面內兩個定點,AB=2c(c是定長),平面內滿足MA* MB=a^2(a是定長)的點M的軌跡稱為卡西尼卵形線。卡西尼卵形線是由天文學家喬凡尼卡西尼提出的。其直角坐標方程為:
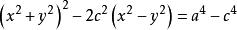 笛卡兒卵形線
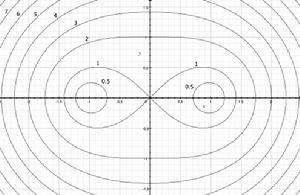
笛卡兒卵形線(1)當a=c時,卡西尼卵形線是雙紐線;
(2)當a<c時,卡西尼卵形線是兩支曲線,隨著a值減小,分別向A、B收縮;
(3)當a>c時,不自交。
笛卡兒卵形線的繪製方法
用matlab
示例:
clear;clc
f=@(x,y,z)(x.^2 + (9/4)*y.^2 + z.^2 - 1).^3 - x.^2.*z.^3 - (9/80)*y.^2.*z.^3;
gd=80;
x=linspace(-3,3,gd);
y=linspace(-3,3,gd);
z=linspace(-3,3,gd);
[x,y,z]=meshgrid(x,y,z);val=f(x,y,z);
[f,v]=isosurface(x,y,z,val,0);
newplot;
p=patch('Faces',f,'Vertices',v,'CData',v(:,3),'facecolor','w','EdgeColor','flat');
h=isonormals(x,y,z,val,p);view(3);set(p,'AmbientStrength',.5);grid on
用Why數學圖像生成工具
 圖3
圖3示例如下,結果如圖3所示 。
pixels = W:1024 H:1024
x = from 0 to 1023 W
y = from 0 to 1023 H
a = 256
b = 512
c = 768
d = 512
u = sqrt((x - a)*(x - a) + (y - b)*(y - b))
v = sqrt((x - c)*(x - c) + (y - d)*(y - d))
m = 0.5
n =0.3
k = m*u + n*v
r = mod(k, 16)/16
g = mod(k, 32)/32
b = mod(k, 48)/48
