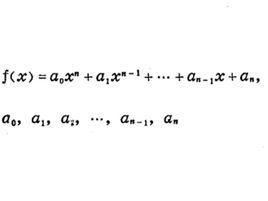基本介紹
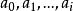 笛卡兒符號律
笛卡兒符號律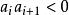 笛卡兒符號律
笛卡兒符號律 笛卡兒符號律
笛卡兒符號律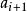 笛卡兒符號律
笛卡兒符號律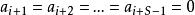 笛卡兒符號律
笛卡兒符號律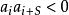 笛卡兒符號律
笛卡兒符號律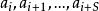 笛卡兒符號律
笛卡兒符號律設為實數序列,如果,則說與間有一個變號,如果, 但,則說有一個變號,例如序列-3,-8,0,2,0,0,4,-5,0共有兩個變號, 而序列0,-1,5隻有一個變號。
笛卡兒符號律 設:
f(x)=ax +ax +…+ax+a,
其實係數序列
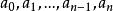 笛卡兒符號律
笛卡兒符號律 笛卡兒符號律
笛卡兒符號律有個變號,而f(x)=0有p個正根,則
(1)p≤μ;
(2)p=μ=偶數。
在不需要精確計算一個方程在某區間內的實根的個數,而只需估計它有多少實根時,套用笛卡兒符號律是比較方便且有效的方法 。
實係數n次方程f(x)=ax +ax +…+ax+a=0的正根的個數等於f(x)中各項的變號數,或者比變號數少偶數個。這裡,m重根應按m個根計算。為了確定負根的個數,可在f(x)中用-x代替x,然後考慮f(-x)。例如,x -x -x -x-1=0的變號數為3,因此這個方程或者有三個正根或者有一個正根。又因為用-x代替x,得到x +x -x -x-1=0,其變號數為1,所以原方程正好有一個負根 。
相關介紹
笛卡兒唯一的數學著作是《幾何學》,書中闡述了他的關於解析幾何的思想,後人把它作為解析幾何學的起點。《幾何學》共分三個部分:第一部分討論了尺規作圖;第二部分討論了曲線的性質;第三部分研究了當時流行的問題。書中第一次提出了變數與函式的概念,這樣就使笛卡兒試圖創建一種幾何與代數的滲透科學。
在《幾何學》中,笛卡兒還研究了代數方程理論,給出了所謂 笛卡兒正負號法則:多項式方程f(x) = 0正根個數不超過係數變號的次數,而負根個數不超過係數的兩個正號和兩個負號連續出現的次數 。
笛卡兒的另一重要研究結果就是現今的因式定理: f(x)能為(x-a)整除,若且唯若a是f(x)= 0的根。此外,笛卡兒還建立了求多項式方程有理根的現代方法,引人了因式分解的待定係數法。這也是中學數學內容中重要的一部分。
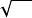 笛卡兒符號律
笛卡兒符號律笛卡兒的數學貢獻還在於,他對韋達所採用的字母符號的表示作出改進。他以英文字母中末尾幾個字母x、y、z.....表示未知數;用開頭幾個字母a、b、....表示已知數。這種表示習慣一直沿襲至今。關於冪的指數的簡單表示法、平方根符號“”也是笛卡兒首先使用的。
笛卡兒在無窮小分析領域對微積分的創立方面都起到了重要的推動作用。現代數學文獻中,有許多概念都是以笛卡兒的名字命名的。如,笛卡兒坐標系、笛卡兒乘積、笛卡兒拋物線、葉形線、卵形線等等。
笛卡兒的想像豐富、觀點新穎,是一位天才的數學家。遺憾的是,他缺少一個健康的體魄。1649年,他應瑞典女王克里斯蒂娜的邀請,前去給她講學。這位女王當年才19歲,有魄力、有見識、又有些“怪癖”。克里斯蒂娜要求笛卡兒每天清晨5點鐘必須在寒冷的圖書倌里為她上課,這就打破了笛卡兒長期形成的、每天早晨臥床“晨思”的生活習慣。數月之後,笛卡兒染上了肺炎。笛卡兒由於經受不了寒冷的侵襲和病魔的折騰,沒過多久,就病逝在瑞典了。笛卡兒去世後的16年,根據法國政府的要求,笛卡兒的遺骨被運回巴黎。舉行了隆重的安葬儀式。
笛卡兒不愧為近代科學的莫基人之一。當他登上科學舞台時,自然科學正醞釀著重大突破。在這個科學發展的重要時期,笛卡兒獨闢蹊徑,他的理論思想促進了數學科學迅速的發展。笛卡兒是西方理性主義的創始人,是近代演繹法的先驅。笛卡兒強調科學方法的重要。他推崇理性,但並不輕視實際觀察。笛卡兒認為整個世界就是一本大書 。