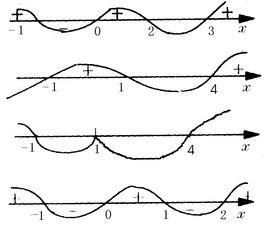
舉例
第一步:通過不等式的諸多性質對不等式進行移項,使得右側為0,並分解因式。(注意:一定要保證x項最高項係數為正數)
例如:將x^3-2x^2-x+2>0化為(x-2)(x-1)(x+1)>0
第二步:將不等號換成等號解出所有根。
例如:(x-2)(x-1)(x+1)=0的根為:x1=2,x2=1,x3=-1
第三步:在數軸上從左到右依次標出各根。
例如:-1 1 2
第四步:畫穿根線:以數軸為標準,從“最右根”的右上方穿過根,往左下畫線,然後又穿過“次右根”上去,一上一下依次穿過各根。
第五步:觀察不等號,如果不等號為“>”,則取數軸上方,穿根線以內的範圍;如果不等號為“<”則取數軸下方,穿根線以內的範圍。
例如:
若求(x-2)(x-1)(x+1)>0的根。
在數軸上標根得:-1 1 2
畫穿根線:由右上方開始穿根。
因為不等號為“>”則取數軸上方,穿根線以內的範圍。即:-1<x<1或x>2。
穿根前應注意, 每項X係數均為正,否則應先則提取負號,改變相應不等號方向,再穿根。例如(2-x)(x-1)(x+1)<0,要先化為(x-2)(x-1)(x+1)>0,再穿根。
奇過偶不過定律
穿根法的奇過偶不過定律:就是當不等式中含有有單獨的x偶冪項時,如(x^2)或(x^4)時,穿根線是不穿過0點的。但是對於X奇數冪項,就要穿過0點了。還有一種情況就是例如:(X-1)^2.當不等式里出現這種部分時,線是不穿過1點的。但是對於如(X-1)^3的式子,穿根線要過1點。也是奇過偶不過。可以簡單記為“ 奇穿過,偶彈回”或“ 自上而下,從右到左,奇次根一穿而過,偶次根一穿不過”。
關於分號的問題
還有關於分號的問題:當不等式移項後,可能是分式,同樣是可以用穿根法的,直接把分號下面的乘上來,變成乘法式子。繼續用穿根法,但是注意,解不能讓原來分式下面的式子等於0
穿根法在函式中的套用
穿根法可以用於函式中,以了解函式圖像的走勢。如:
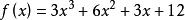 穿根法
穿根法先求出f(x)的導數
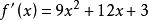 穿根法
穿根法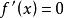 穿根法
穿根法令: ,有
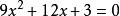 穿根法
穿根法 穿根法
穿根法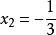 穿根法
穿根法解得 ,
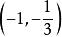 穿根法
穿根法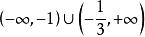 穿根法
穿根法再由穿根法,可知,f '(x)在 上小於 0,在 大於0,即:
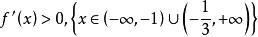 穿根法
穿根法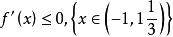 穿根法
穿根法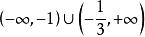 穿根法
穿根法 穿根法
穿根法由此知函式在 為 ,
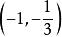 穿根法
穿根法 穿根法
穿根法在 為 。
從而知道了函式的走勢。