穩定性概念
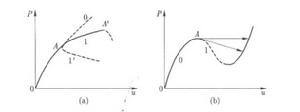
結構從穩定平衡轉變為不穩定平衡稱為失穩(或屈曲)，發生穩定性改變的平衡狀態稱為臨界狀態。結構失穩有分支屈曲和極值點屈曲兩種類型，見圖，圖中實線為穩定平衡，虛線為不穩定平衡。分支屈曲的解路徑f載荷一位移曲線)在臨界點(分支點)A處存在穩定或者不穩定分支(圖1(a)中路徑1或1’)。
圖一極值點屈曲的臨界點(圖1(b)中A點)是載荷的極值，在臨界點前後為同一路徑，平衡狀態常常發生大範圍改變，跳向另一個穩定平衡，所以也稱為“跳躍”失穩。臨界點之後的平衡稱為後屈曲狀態，在後屈曲路徑上可能發生新的屈曲稱為二次屈曲(例如圖1(a)中的A7點)，二次屈曲也有兩種類型。軸壓直桿和平板的屆曲是分支屈曲，小曲率淺拱和扁球蓋受外壓作用時可發生極值點屈曲。軸壓平板在屈曲之後可能發生二次分支屈曲，表現為後屈曲形態的突然變化，壓桿屈曲之後由於塑性變形可以出現載荷的極值點。
穩定性定義
動力準則
彈性系統平衡穩定性是根據受到小擾動之後系統運動是否有界定義的。
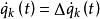穩定準則假設一個系統有n個自由度qk(k=1，…，n)，在給定載荷作用下系統的平衡位置為q'，若系統受到小干擾作用，在干擾去掉之後的自由運動位置為qk(t)=q'+△qk(t)，速度為 。
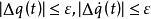穩定準則如果總是能夠選擇足夠小的初始干擾△qk(0)和△qk'(0)，使得以後的運動限制在任意小的範圍內，即 ，(ε是給定的任意小正數)，則系統的平衡狀態q'是穩定的，否則是不穩定的。
上述穩定性定義也稱為Lyapunov動力準則。實際結構一般是連續系統，有無限多個自由度。嚴格地講，不能將有限自由度的結果簡單地推廣用於無限自由度情況，能否將動力準則推廣到連續體的問題仍在討論。但是，在多數情況下，這種推廣是可靠的。
套用動力準則確定臨界點和判斷平衡穩定性，需要用動力學方法研究系統的動力特性，在大多數實際問題中這一方法並不方便。更為簡便的是靜力(平衡)法和能量法，相應的穩定準則是靜力準則和能量準則。
靜力準則
在分支點附近，除原來的平衡狀態外還存在其他平衡狀態。因此，當完善(無缺陷)系統有一個微小的附加位移時(嚴格說來是無限小可能位移)，在同樣載荷作用下，系統將可能在新的鄰近狀態處於平衡，則該點必為分支點，這一準則稱為靜力準則。
對於非完善(有微小缺陷)系統，當載荷趨近完善系統的分支點時，線上性穩定理論範圍內，系統的變形趨於無限大，此時靜力準則也稱為微擾動準則。
套用靜力準則求臨界載荷時，只需建立無限鄰近狀態的平衡方程和邊界條件，由於原始狀態(或基本狀態)是平衡的，所以附加位移滿足齊次方程和邊界條件，構成特徵值問題，特徵函式稱為屈曲形態，特徵值即為臨界載荷。靜力準則給出了分支點條件，套用比較簡單，對於保守系統可以得到與動力準則相同的結果，但不能判斷平衡本身的穩定性。
能量準則
判斷保守系的臨界狀態和穩定性可以套用能量準則。若彈性保守系統失穩前平衡狀態I(基本狀態)的位能為PⅠ，考慮任一個可能的鄰近狀態Ⅱ，位能為PⅡ，
平衡狀態I穩定的充分必要條件是P為最小值，即對於所有的鄰近狀態
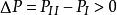穩定準則反之，若至少有一個鄰近狀態，使
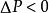穩定準則則平衡狀態I 是不穩定的。上述穩定性準則稱為能量準則。若運動許可的微小附加位移(即位移的變分)記作：
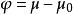穩定準則
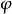穩定準則式中，u，uo是狀態Ⅱ和Ⅰ的位移，則位能增量泛函△P可以展成 的Taylor級數：
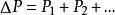穩定準則
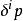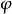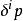穩定準則 穩定準則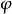 穩定準則 穩定準則式中，PI是 的i次泛函(或記作 ，i=1，2，…)，即 (及其導數)的i次項，或j次變分。由於I是平衡狀態，位能駐值原理給出=P1=0，所以
△P=P2+P3+…
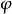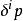穩定準則 穩定準則因為 是無限小量，一般情況下△p的符號決定於P2(或 )，可表為：對於所有幾何可能的，
P2>0
所以，位能的二次變分恆正是穩定的充分條件；而
P2≥0
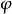穩定準則即位能的二次變分非負是穩定的必要條件；如果P2=0僅對 =0成立，上式也是充分條件。由於略去了高次項，用二次變分表示的能量準則更方便。
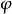穩定準則為求臨界狀態的變分方程，也稱為中性平衡方程。由於P2是 (及其導數)的二次齊次泛函，所以其歐拉方程是齊次的，歸結為特徵值問題。求解特徵方程式，可以得到特徵值(臨界載荷)及對應的特徵函式(屈曲形態，也稱為屈曲模態)。同一臨界載荷只有一個屈曲模態時稱為單模態問題，有多個屈曲模態時稱為多模態問題。歐拉方程與根據靜力準則建立的微擾動平衡方程相同。
對於保守系而言，上述三個穩定準則給出相同的結果，是等價的；研究非保守系統的穩定性應該採用動力準則。
