內容及自由度
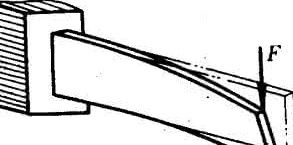
結構的穩定自由度計算不論是研究第一類或第二類的穩定性，穩定計算的中心內容都是要確定結構的臨界荷載，據此對結構進行必要的穩定性驗算，以確保其安全。
在穩定計算中，涉及結構穩定自由度的概念。結構的穩定自由度是指當結構失穩時為了確定其變形形狀所需的獨立坐標數數目。例如，右圖(a)裝有抗轉彈簧支座的剛性壓桿，失穩後的變形狀態如圖中虛線所示，它僅需一個獨立坐標口就可確定其失穩模態，因此它是一個自由度；右圖(b)所示為由兩根抗移彈簧在中間相連三根剛性壓桿，確定其失穩模態的獨立坐標為y、y，故知其是兩個自由度；右圖(c)所示為兩端鉸支且EI=∞的彈性壓桿，需要無限多個獨立坐標y才可確定其失穩模態，故它為無限自由度。
目的
圖1 細長壓桿結構因各種外因作用而產生的內力與位移的計算問題涉及結構的強度與剛度的計算問題。但是，要確保結構設計符合既經濟又安全的原則，僅有上述兩方面的計算是不全面的，還必須考慮結構的穩定計算。
關於穩定計算的概念，是完全不同於強度、剛度的計算。例如，若施力壓一根粗短的桿件就不易被壓彎，在繼續施力後，當其橫截面上的工作應力超過材料的極限強度時，該粗短桿即因強度不足失去其繼續承載的能力而遭破壞。然而，當施力去壓一根細長桿時，桿就很容易被壓彎，如圖1所示。若令其橫截面面積與上述的粗短桿一樣，則細長桿被壓彎時所需施加的軸向壓力，也遠遠小於粗短桿因強度破壞時所需施加的軸向壓力。此刻，細長桿的工作應力可能還遠未抵達材料的極限強度，甚至還低於材料的比例極限時，就會因突然屈曲而喪失其承載能力，這種現象就是通常所說的失穩。因此，粗短桿受壓時的承載能力則由強度條件所決定；而細長桿受壓時的承載能力則由穩定性條件所決定。
細長壓桿存在著失穩問題，對其他類型的結構也同樣有失穩問題尚待研究。在工程實踐中，因忽視穩定問題而造成工程事故的例子並不少見。例如，1922年美國華盛頓鎳克爾卜克爾劇院，在一場特大雪中倒塌，究其原因是屋頂結構中的一根梁由於負荷過大而引起失穩；再如1925年前蘇聯莫茲爾橋，在試車時由於橋樑桁架個別壓桿失穩而造成事故，等等。隨著科技事業的進步，很多建築結構有逐步向高層、大跨度、薄壁方向發展的趨勢，因此對結構穩定問題的深入探討顯得更為迫切，因此它具有像研究結構強度、剛度問題同樣的重要性。
平衡類型
圖2 剛性小球常用圖2所示剛性小球在不同位置上的平衡說明穩定性的概念。雖然小球在圖示的三種情況下都是平衡的，但是它們之間存在著差別。
如果對圖2(a)的小球做微小的干擾，則小球就離開凹形曲面最低點的初始平衡位置，進行若干次來回擺動，最後仍回復到它初始的平衡位置，則稱這個小球的初始平衡位置是處於穩定平衡狀態。
若對圖2(b)在凸形曲面最高點處的小球做微小的干擾，小球就離開其初始平衡位置，當干擾力解除後，小球不僅不能回到初始平衡位置，而且還將繼續遠離該位置。因此，小球處於凸形曲面最高點處的初始平衡位置，是處於不穩定平衡狀態。
圖2(c)所示為在平面上的小球，對其作微小干擾後，小球就離開靜止時的初始平衡位置，滾動一段小距離後在新位置上停留並處於新的平衡位置，它既不能回到初始平衡位置，也不繼續離開新的平衡位置，具有這種特性的平衡稱為隨遇平衡狀態或臨界平衡狀態。隨遇平衡是由穩定平衡過渡到不穩定平衡的一種臨界平衡狀態，人們研究結構的穩定性．正是利用了這種平衡狀態的特性。實質上，隨遇平衡可歸入不穩定平衡狀態的範疇。因為圖2(c)所示的小球受微小干擾後就不再回到原有的初始平衡位置上。
上述剛性小球的三種平衡形式，在研究彈性體的穩定性時也同樣存在。
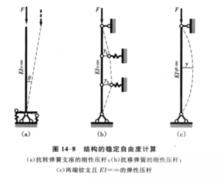
圖3(a)所示的懸臂細長桿，桿端所施加的軸向壓力F若小於某個特定的荷載值F時，由於水平干擾的外因作用使懸臂桿彎曲，但該干擾解除後，懸臂桿搖動若干次後仍將回復到它原來的直線位置上保持平衡，而不能占有其他位置，這種直線平衡形式是處於穩定平衡狀態的，它類似圖2(a)的情況。
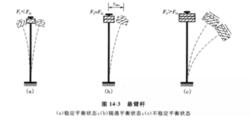圖3 懸臂桿若在桿端繼續載入至F數值，且F=F[見圖3(b)]，懸臂桿雖然暫時保持著直線平衡形式，但只要給以微小的干擾，它將立即向一邊發生微小彎曲，在新位置上處於平衡，當干擾解除後，它既不回到原有的直線平衡位置，也不進一步擴大變形，而是停留在微彎的位置上。這一情況類似於圖2(c)所示的隨遇平衡或臨界平衡狀態。隨遇平衡狀態具有平衡的二重性質，或者說出現了平衡形式的分支；就如圖3(b)所示的情況，懸臂桿既可在不受干擾時暫時保持只受軸向壓力的直線形式平衡，也可保持同時受壓和受彎的微彎形式平衡。但在實際工程中，由於材料的不均勻性，非理想的直桿或施加荷載時難以避免的偏心等缺陷，將無形起著側向干擾的作用，因此當F=F時，原有的直線平衡形式實際上將開始成為不穩定的平衡狀態，定義這個特定荷載值F為臨界荷載。因此，臨界荷載是使結構原有平衡形式保持穩定的最大荷載，也是使結構產生新的平衡形式時的最小荷載。採用這個準則用以計算臨界荷載的方法通常稱為隨遇平衡法。
研究繼續載入後的情況，即當F>F[見圖3(c)]，變形將迅速擴大，致使懸臂桿完全喪失承載能力而破壞，這一情況類似於圖2(b)。
綜上所述，當F<F時，懸臂桿處於穩定平衡狀態；當F>F時，懸臂桿處於不穩定平衡狀態；當F=F時，懸臂桿處於隨遇平衡或臨界平衡狀態。由此可知，隨著軸向壓力F的量變，將引起平衡狀態穩定性的質變。
失穩現象
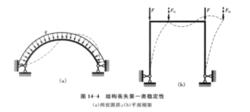圖4 結構喪失第一類穩定性結構的失穩現象可分為兩類。圖3所示的失穩現象，常稱為喪失第一類穩定性，或稱為分支點失穩。例如圖3(a)所示的懸臂桿，當F<F時，僅有與承受軸向壓力相應的軸向變形產生；但當F=F時[見圖3(b)]，除產生與受壓相應的軸向變形外，還將產生與受彎相應的彎曲變形。因此，在內力和變形的性質上都起了質變。
第一類穩定性也可以這樣來進行描述：當F<F時，懸臂桿一直保持只受軸力的直線平衡形式[見圖3(a)]；當F=F時，出現了平衡分支現象，即懸臂桿既可以保持原來只受軸力的直線平衡形式，也可以有一個新的不定幅值的同時受壓和受彎的彎曲平衡形式[見圖3(b)]，其中，y為懸臂桿的頂點水平位移。這一特性標誌著當F=F時出現了臨界平衡狀態，它是處在由穩定平衡向不穩定平衡過渡的臨界點上。
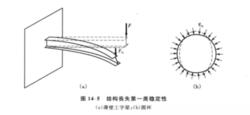圖5 結構喪失第一類穩定性喪失第一類穩定的現象，在其他結構中同樣也可出現。例如，圖4(a)所示為在靜水壓力作用下處於軸心受壓狀態的圓拱。當水壓力q小於其臨界值q時，它維持圓形的平衡形式。當q達到q時，這種變形形式就成為不穩定的，由於某種擾動，即可能出現一種新的類似波浪形的變形形式，如圖中虛線所示。對於圖4(b)所示的平面剛架，當荷載F<F時，剛架柱處於軸心受壓狀態而只有壓縮變形；當荷載F=F時，剛架原來的平衡狀態變成不穩定的，由於某種擾動，即將出現如圖中虛線所示的變形形式。由上可知，對於喪失軸心受壓的穩定，其特點是體系的變形形式發生質的變化，出現了具有壓縮和彎曲兩種變形的形式。
圖5(a)所示的薄壁工字梁，當荷載F<F時，梁在荷載作用的豎向平面內發生彎曲變形，即保持平面彎曲的平衡形式。當荷載F=F時，平面彎曲形式的平衡成為不穩定的，此時梁可能出現一種新的平衡形式：梁將偏離原來荷載作用的平面而發生斜彎曲和扭轉，如圖5中實線所示，即喪失了平面彎曲形式的穩定。再如承受靜水壓力作用的圓環[見圖5(b)]，當荷載q未抵達臨界值q前，結構中僅承受軸向壓力，將保持原有結構形狀上的穩定平衡，當荷載q抵達臨界值q時，原有結構的平衡形式將成為不穩定的，將出現如圖中虛線所示的平衡形式。
綜上所述可知，喪失第一類穩定性的特徵：結構的變形產生了性質上的突變。即原來的平衡形式成為不穩定的，而可能出現新的與原來平衡形式有質的區別的平衡形式，同時，這種現象是帶有突然性的。
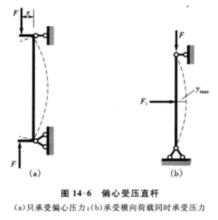圖6 偏心受壓直桿除上述喪失第一類穩定性的情況外，尚有喪失第二類穩定性的情況，這是兩種性質不一樣的穩定性概念。這類喪失穩定的特徵是結構原來的變形將大大發展，而不會出現新的變形形式。即結構的平衡形式並不發生質變，但由於變形的增大，結構將不能正常工作。例如，圖6(a)所示為兩端鉸支承受偏心壓力F的直桿，當桿件開始受力時即同時處於受壓和受彎狀態，並伴生了撓度。荷載與撓度之間的關係如圖7所示。當F<F時，若不繼續增大荷載，則桿件的撓度也不增加。但當F值抵達F後，即使不再繼續增加荷載甚至減小荷載，撓度仍將繼續增大，稱這種現象為喪失第二類穩定性。載入至極值點A時的荷載值F即為喪失第二類穩定性的臨界荷載。因此，又把喪失第二類穩定性稱為極值點失穩，顯然，它與喪失第一類穩定性相比具有不同的概念。圖6(b)所示為承受橫向荷載F（假定F保持常量）同時承受壓力F作用的壓彎桿件，失穩時也有類似於偏心壓桿的特徵。
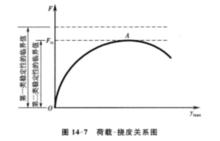圖7 荷載-撓度關係圖綜上所述，喪失第二類穩定性的特點為：平衡形式並不發生質的變化，隨著荷載F的逐漸增加，變形僅以量變的形式迅速增長，最後使結構喪失承載能力。
喪失第二類穩定性時的臨界值實際上要低於喪失第一類穩定性時的臨界值，這是因為桿件在偏心受壓或壓彎的情況下，隨著荷載F的不斷增加，截面的邊緣纖維應力將首先抵達屈服極限，引起局部的塑性變形，使截面進入彈塑性階段的工作狀態，而塑性變形擴展的結果，就導致桿件承載能力的降低。
作用於結構上的荷載，一般並非都使桿件產生軸向受壓，例如，受壓彎作用的剛架柱、壓力曲線不與拱軸相重合的各類拱結構、非理想桁架中的某些桿件等。因此，工程中的穩定問題實際上均屬於第二類穩定性問題。研究第二類穩定性要涉及多種因素的影響，首先荷載一位移關係是幾何非線性的，其次有時還要考慮到材料的非線性性質。因此，它比第一類穩定要複雜得多。為了計算簡便起見，可針對結構的荷載作用方式作某些簡化假定，將第二類穩定化為第一類穩定來處理，並通過某些係數反映兩類穩定問題之間的差別。
對於工程結構來說，喪失上述兩類穩定性都是不能允許的。
