程式邏輯
正文
描述和論證程式行為的邏輯，又稱霍爾邏輯。程式和邏輯有著本質的聯繫。如果把程式看成一個執行過程，它接收一些信息，又輸出一些信息。用邏輯公式描述對輸入和輸出信息的要求，就可以建立邏輯公式和程式間的聯繫，表示為｛P｝S｛Q｝
其中P和Q為有關程式變元的邏輯表達式；P稱為S的前置條件；Q稱為S的後置條件。此公式表示:如果程式S執行前程式變數的值滿足前置條件P，且程式S終止，則程式S執行終止後，程式變數的值滿足後置條件Q。如果進一步建立一套關於這類公式的推理規則，就能得到一個描述程式行為的邏輯系統，可以在此系統中研究程式的性質，這就是程式邏輯。程式是在機器中執行的，程式中每個語句的執行導致機器狀態的變化，因此程式的執行又可以由機器狀態變化的序列表達。數理邏輯中的模態邏輯正是描述動態變元變化的一種邏輯，因此以模態邏輯為基礎也可揭示邏輯與程式間的深刻聯繫。
歷史和發展 美國R.W.弗洛依德於60年代中期把框圖程式對應為邏輯公式，提出使用邏輯描述和分析程式的想法。1969年前後英國C.A.R.霍爾首次給出一類程式語言的邏輯系統，提出程式部分正確性的形式驗證規則（見程式驗證）。70年代初，波蘭和瑞士一些學者提出使用算法邏輯描述和分析程式，這是第一次把模態邏輯引入程式邏輯的嘗試。70年代中期，有些科學家進一步提出使用動態邏輯和時態邏輯，描述和論證程式，推動了程式邏輯的研究。
基本方法 程式邏輯的基本方法是先給出建立程式和邏輯間聯繫的形式化方法,然後建立程式邏輯系統,並在此系統中研究程式的各種性質，例如，在霍爾邏輯中，程式邏輯公式的形式為
｛P｝S｛Q｝
如上所述,這類公式不能表示S的終止特性，因此霍爾邏輯是討論程式部分正確性的邏輯。如果在霍爾邏輯系統中可以證明｛P｝S｛Q｝,同時又能證明對滿足前置條件的所有輸入變數程式S都終止，則稱程式具有完全正確性。在公式｛P｝S｛Q｝中邏輯表達式P和Q實際上只是當作語句S的注釋使用的,對邏輯公式｛P｝S｛Q｝不能進行邏輯運算，例如蘊含公式｛P1｝S1｛Q1｝→｛P2｝S2｛Q2｝就沒有意義，因此霍爾邏輯還沒有徹底把程式和邏輯統一起來。解決的方法之一就是使用動態邏輯，它是一種模態邏輯。在動態邏輯中除了通常的命題連線詞 墯,∨,∧,→及作用於非動態變元的量詞
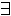和凬外,還可以引入動態連線詞,例如【 】，【S】Q表示當S 終止時Q為真。這樣墯【S】Q，【S1】P→【S2】Q等就都是有意義的邏輯公式,如果進一步令〈 〉表示墯【 】墯，則<S>Q表示存在一個時刻S終止且Q為真。程式S的部分正確性問題就可以表示為 P →【S】Q
即P真蘊含當S終止時Q為真。如果S是確定性語句，則其完全正確性問題可以表示為P →<S>Q
即P真蘊含S在某一時刻終止且Q真。霍爾邏輯的基本思想是用邏輯描述程式的執行結果，與之對應的另一種方法是用邏輯刻畫程式的全部行為，即把程式的執行過程看成機器狀態的一個變化序列。自70年代中期，並髮式程式設計逐漸成為程式理論的重要課題後，這種觀點就顯得十分必要，因為刻畫在程式執行過程中，各任務之間的同步和信息交換常常是不可少的。時態邏輯是關於隨著時間而不斷改變其值的動態變元（叫作時序變元）的一種模態邏輯。因此它自然地被引入到程式邏輯中。時態邏輯以當前時間為基本出發點，除使用常用邏輯連線詞及作用於非時序變元的量詞外，還可以用引入時態連線詞的辦法刻畫更複雜的動態性質。例如，可以引入連線詞◇及□：
◇P 表示在將來某一時刻P真，
□P 表示P從此以後永真。
使用時態邏輯可以對每個程式構造出它所對應的一個邏輯系統，並可以在此系統中刻畫終止（記作STOP）及無死鎖等概念。而程式S 的部分正確性問題就可以表示為
P →□(STOP →Q)
在程式S 所對應的邏輯系統中成立,即程式開始執行時P真蘊含如果將來任一時刻程式終止則Q真,而其完全正確性則可表示為P →◇(STOP&Q)
在該邏輯系統中成立,即程式開始執行時P真蘊含存在某一時刻S 終止並且Q真。套用 由於程式邏輯使用邏輯系統描述程式的行為，它與具體執行程式的機器無關，因此程式邏輯的研究為公理語義學提供了理論基礎。在邏輯系統中又可以分析和論證程式的性質，因此它又是程式驗證的理論基礎。
現代軟體工程的一個重要方法是在程式設計之前，必須把程式要達到的目標即功能描述交待清楚。功能描述應當簡潔明瞭，而不必關心執行細節，因此可以使用邏輯語言的全部公式。
程式設計的任務就是編製程序使其滿足描述。程式邏輯的研究表明，程式和邏輯都可以作為邏輯系統的邏輯公式，所不同的是程式只出現在一部分特定的邏輯公式中。因此設計程式使之滿足描述的過程，從邏輯演算角度看，就是如何將表示功能描述的邏輯公式轉化成表示程式的邏輯公式問題，因此程式邏輯的研究又為軟體工程中自動化設計提供了有力工具。
