起源
這個想法起源於羅伯特·弗洛伊德於較早的研究,他為流程圖提供了類似的系統。東尼·霍爾於1969年首次發表[,隨後為其他研究者所精製。
Hoare 邏輯(也叫做 Floyd–Hoare 邏輯)是英國計算機科學家C. A. R. Hoare開發的形式系統,隨後為 Hoare 和其他研究者所精製。它發表於 Hoare 1969年的論文"電腦程式的公理基礎"中。這個系統的用途是為了使用嚴格的數理邏輯推理電腦程式的正確性提供一組邏輯規則。
Hoare 認可 Robert Floyd的早期貢獻,他為流程圖提供了類似的系統。
霍爾三元組
霍爾邏輯的中心特徵是霍爾三元組(Hoare triple)。這種三元組描述一段代碼的執行如何改變計算的狀態。Hoare三元組有如下形式
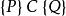 霍爾邏輯
霍爾邏輯這裡的 P和 Q是 斷言而 C是 命令。 P叫做 前條件而 Q叫做 後條件。斷言是謂詞邏輯的公式。這個三元組在直覺上讀做:只要 P在 C執行前的狀態下成立,則在執行之後 Q也成立。注意如果 C不終止,也就沒有"之後"了,所以 Q在根本上可以是任何語句。實際上,你可以選擇 Q為假來表達 C不終止。事實上,這種情形叫做 "部分正確(partial correctness)"。如果 C終止並且在終止時 Q是真,則表達式被稱作 "全部正確性(total correctness)"。終止必須被單獨證明。
霍爾邏輯為簡單的命令式程式語言的所有構造提供了公理和推理規則。除了給Hoare論文中的簡單語言的規則,其他語言構造的規則也已經被Hoare和很多其他研究者開發完成。包括並發、過程、goto語句,和指針。
命令式編程
命令式編程(英語:Imperative programming),是一種描述計算機所需作出的行為的編程典範。幾乎所有計算機的硬體工作都是命令式的;幾乎所有計算機的硬體都是設計來運行機器代碼,使用命令式的風格來寫的。較高端的命令式程式語言使用變數和更複雜的語句,但仍依從相同的典範。菜譜和行動清單,雖非電腦程式,但與命令式編程有相似的風格:每步都是指令,有形的世界控制情況。因為命令式編程的基礎觀念,不但概念上比較熟悉,而且較容易具體表現於硬體,所以大部分的程式語言都是命令式的。
