基本介紹
方差分析法和秩方差分析法,都是多個樣本齊一性的統計檢驗方法,區別在於,1. 方差分析法,要求產生樣本的總體具有正態性和等方差性,要求檢驗參數假設“各總體均值相等”;而秩方差分析法不要求正態性和等方差性, 要求檢驗非參數假設“各樣本來自同一總體”;2.方差分析法直接對觀測值進行分析,而秩方差分析法觀測值的秩進行分析 (也可能對經正態變換的秩進行分析)。
舉例介紹
Friedman檢驗
在比較三個以上樣本大小關係的非參數統計檢驗中,有兩類基本設計。第一種設計涉及若干獨立的隨機樣本。這些樣本的樣本量可以相同也可以不同,而且每個樣本中的每個個體與其它樣本中的任何個體無對應關係。這種檢驗多個獨立總體大小的非參數方法主要有Kruskal-Wallis檢驗和推廣的中位數檢驗。第二種設計所考查的樣本中的每個個體都具有完全相同的樣本量,而且各樣本中的每一個體都與其它樣本中的相應個體具有對應關係。這類數據中包含的信息顯然多於獨立樣本。Friedman檢驗(Friedman’s ranktest),又稱Friedman隨機區組秩方差分析(Friedman's methodfor randomized blocks)就屬於此類方法。它能夠充分利用相關樣本中的全部信息。從理論上說,使用Kruskal-Wallis檢驗與推廣的中位數法判斷多個相關樣本是否來自大小有明顯差異的總體也不失正確,但這種做法就像用檢驗兩個獨立樣本的非參數方法,如Mann-Whitney U一檢驗或者Kolmogorov單側檢驗來比較兩個相關樣本大小一樣,必然會忽略樣本中關於不同個體間差別的信息,從而降低檢驗功效,這當然是研究者不希望發生的。
雖然到目前為止還不了解Friedman檢驗的準確功效效率,但由於它充分利用了原始數據中的信息,其功效應當很接近相應的參數方法。
對三個以上相關樣本進行Friedman檢驗的原假設和對立假設與兩種多個獨立總體大小比較方法相同,記為:
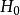 秩方差分析
秩方差分析:多個樣本來自大小沒有明顯差異的總體,
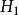 秩方差分析
秩方差分析:多個樣本來自大小有明顯差異的總體。
對於Friedman秩方差分析,由於樣本之間具有相關關係,因而不能像Kruskal-Wallis法那樣將所有樣本放在一起排序,而只能利用不同樣本中個體間的對應關係,分別對每一對應數據組中的k個數據求秩。對待檢驗的k個樣本量均為n的樣本:
 秩方差分析
秩方差分析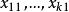 秩方差分析
秩方差分析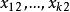 秩方差分析
秩方差分析依次對樣本中的第1,2…n個數據組排序。即先對 獨立排序,再對 排序,依此類推,最終得到n組(每組k個)秩數據:
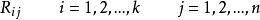 秩方差分析
秩方差分析k個樣本的秩和分別是:
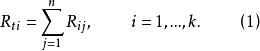 秩方差分析
秩方差分析再按下式計算檢驗值:
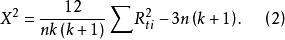 秩方差分析
秩方差分析 秩方差分析
秩方差分析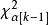 秩方差分析
秩方差分析根據事先確定的顯著性水平( )以及自由度(k-1),從表中查得檢驗的臨界值 ,如果
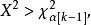 秩方差分析
秩方差分析便可以拒絕檢驗的原假設。
在樣本量較小的情況下,以上計算結果明顯偏離卡方分布。此時需利用專門的臨界值表進行檢驗。如果計算值大於臨界值:
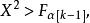 秩方差分析
秩方差分析可以拒絕檢驗原假設。
對於涉及6個以上總體的小樣本量Friedman檢驗,如果不能從有關書籍中查到臨界值,便只能採用卡方檢驗了。
克魯斯卡爾-沃利斯檢驗
方差分析(ANOVA)程式關注的是,幾個總體的均值是否相等。數據是間隔測量尺度或比率測量尺度的數據。另外還要假定這些總體服從正態機率分布,並且有相等的標準差。如果數據是順序測量尺度的和(或)總體不服從常態分配會怎樣呢?W.H.克魯斯卡爾(Kruskal)和W.A.沃利斯(Wallis)於1952年提出了僅僅要求順序(排序)測量尺度數據的非參數檢驗。不需要對總體分布形態做任何假定。該檢驗被稱為克魯斯卡爾-沃利斯單因素秩方差分析(Kruskal-Wallis one-way analysis of variance by ranks)。
為了利用克魯斯卡爾-沃利斯檢驗,從總體中抽取的樣本必須是獨立的。例如,從三個組(經理、員工、管理人員)中抽取樣本,並且進行訪談。一組人員(如經理)的回答決不能影響其他兩組的回答。
為了計算克魯斯卡爾-沃利斯檢驗統計量:①合併所有的樣本;②將合併後的樣本值從低到高排序;③將排序後的值用秩代替,從最小值1開始。