簡介
科茨螺線是一種特殊曲線,指極坐標方程為p=asinρθ或p=acosρθ的曲線,即玫瑰線。
根據三角函式的特性可知,科茨螺線是一種具有周期性且包絡線為圓弧的曲線,曲線的幾何結構取決於方程參數的取值,不同的參數決定了玫瑰線的大小、葉子的數目和周期的可變性。這裡參數a(包絡半徑)控制葉子的長短,參數n控制葉子的個數、葉子的大小及周期的長短。
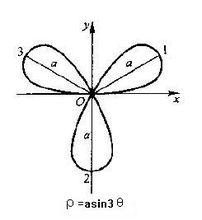 三葉玫瑰線
三葉玫瑰線分類
對於方程式ρ=5sin(3θ)、ρ=5sin(2θ)、ρ=5sin(3θ/2),分別對應的是三葉、四葉和六葉玫瑰線。
玫瑰線總面積(a=π)
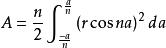 科茨螺線
科茨螺線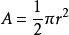 科茨螺線
科茨螺線參數特性
科茨螺線的參數主要是a、n及θ,其值的大小決定科茨螺線的形狀,包括葉子數、葉子長度寬度和曲線閉合周期。係數a只跟葉子的長度有關,而n和θ則影響科茨螺線的多樣性和周期性。通過計算機對方程式ρ=asin(nθ)的大量試驗,證明科茨螺線具有如下三個特性:
1、當n為整數時,若n為奇數,則玫瑰線的葉子數為n,閉合周期為π,即θ角在0-π內玫瑰線是閉合的。當n為偶數時,玫瑰線的葉子數為2n,閉合周期為2π,即θ角取值在0-2π內玫瑰線才是閉合和完整的。
2、當n為非整數的有理數時,設為L/W,且L/W為簡約分數,此時,L與W不可能同時為偶數。L決定科茨螺線的葉子數,W決定科茨螺線的閉合周期(Wπ或2Wπ,見特性3)及葉子的寬度,W越大,葉子越寬。但W也會同時影響葉子數的多少,對同一奇數值L,在W分別取奇數和偶數值時,葉子數也是不同的。
3、當L或W中有一個為偶數時,科茨螺線的葉子數為2L,閉合周期為2Wπ。當L或W同為奇數時,科茨螺線的葉子數為L,閉合周期為Wπ。換句話說,生成偶數個葉子的科茨螺線,L或W中必須有且只有一個為偶數值,且L為葉子數的一半,而生成奇數個葉子的玫瑰線,L和W都必須為奇數,且L值就是葉子數。
特殊情況
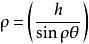 科茨螺線
科茨螺線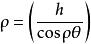 科茨螺線
科茨螺線以極點為反演極的反演圖形或。
當p=1/3時是麥克勞林三等分角曲線。
當p=2時是十字線。
