破圈法

破圈法，是區別於避圈法（Prim算法和Kruskal算法）的一種尋找最小生成樹的算法，也就是MST的一種方法。破圈法是“見圈破圈”，即如果看到圖中有一個圈，就將這個圈的邊去掉一條，直至圖中再無一圈為止。

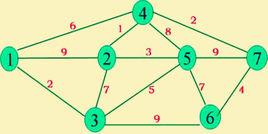
求最小生成樹有兩種方法，一種是破圈法，另一種是避圈法（Kruskal,Prim也是求MST的算法）。

破圈法是“見圈破圈”，即如果看到圖中有一個圈，就將這個圈的邊去掉一條，直至圖中再無一圈為止。

步驟如下：

在圖中找一個迴路

去掉該迴路中權值最大的邊，但要保持圖仍為連通。

反覆此過程，直至圖中再無迴路（但仍保持連通），得到最小生成樹。

1.

在圖中找一個迴路

2.

去掉該迴路中權值最大的邊，但要保持圖仍為連通。

3.

反覆此過程，直至圖中再無迴路（但仍保持連通），得到最小生成樹。

最後結果根據操作選取不同可能不唯一，但圖的權值和（生成樹的代價）相同，均為最小值。

避圈法則採取先將圖中的點都取出來，然後，逐漸向上面添邊，並保證後添入的邊不與以前添上的邊構成圈就可以了，這個過程直到將邊集中能加入的邊（加入後不夠成圈）都加完為止。參見詞條“Prim算法”和“Kruskal算法”。

註：其中破圈法和避圈法的" 圈"指的是迴路