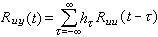介紹
通過對系統輸入和輸出的相關函式之間的關係進行分析建立系統的數學模型。這種方法可以比較有效地克服系統輸出中含有的隨機噪聲給建模帶來的困難。適當選擇輸入,使它與噪聲成為統計不相關的,就可通過相關運算把系統的輸入輸出關係轉變為輸入自相關和輸入輸出互相關的關係,從而消除系統噪聲的影響,使建模更為容易。
分析法
隨機系統的建模有兩種常用的相關分析法。第一種是以脈衝回響(見過渡過程)為模型,連續系統和離散系統的輸入與輸出可以通過脈衝回響聯繫起來,它們的數學表達式分別是
。於是隨機性的輸入與輸出之間的關係被確定性的自相關函式與互相關函式之間的關係所代替,這就是著名的維納-霍夫方程 (見維納濾波)。在適當地選擇輸入,求得輸入自相關函式和輸入輸出互相關函式之後,只須解出維納-霍夫方程就可以得到隨機系統的脈衝回響模型。第二種隨機系統模型是自回歸模型:yt=a1yt-1+a2yt-2+…+anyt-n+εt,式中{yt}是系統的平穩輸出序列,{εt}是白噪聲序列,yt與εt,εt+1,…是統計不相關的,a1,a2,…,an是模型中待估計的係數。對於這種模型,相關分析法建模是利用輸出序列{yt}的自相關序列{rj=E【yt,yt+j】,j=0,1,2,…}求得係數a1,a2,…,an的估計值,最後得到隨機系統的自回歸模型。