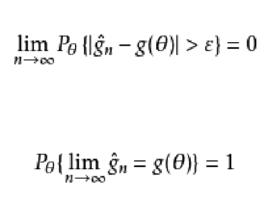基本介紹
無偏性和有效性都是在樣本容量n固定的前提下提出的,當希望隨著樣本容量的增大,一個估計量的值能夠穩定在待估參數真值的附近,這就是估計量的相合性的要求。
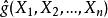 相合性
相合性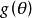 相合性
相合性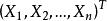 相合性
相合性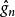 相合性
相合性設為的基於樣本的的一個估計量,顯然它依賴於樣本n,為表明這種依賴性,可以記之為。隨著樣本量的變化,可得到一列估計量,一個自然的希望是,當樣本容量無限增加時,估計量能夠依某種意義接近於被估計量的真值。顯然,這是對估計量的起碼要求。相合性就是這樣的一個要求。
弱相合估計
 相合性
相合性 相合性
相合性 相合性
相合性 相合性
相合性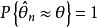 相合性
相合性簡稱“相合估計”。稱為的弱相合估計,如果依機率收斂於,即當n充分大時,有。
強相合估計
 相合性
相合性 相合性
相合性 相合性
相合性 相合性
相合性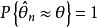 相合性
相合性稱為的強相合估計,如果以機率1收斂於,即當n充分大時,有。
r階相合估計
 相合性
相合性 相合性
相合性 相合性
相合性 相合性
相合性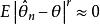 相合性
相合性 相合性
相合性 相合性
相合性稱為的r階相合估計,如果r階收斂於,即當n充分大時,有。特別,當r=2時,稱為的 均方相合估計。
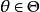 相合性
相合性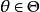 相合性
相合性上述三種相合性之間的關係與三種收斂性的關係是完全一致的。上面的定義中,收斂性指對於任意固定的收斂。假設相應的收斂關於是一致的,則相應的相合性稱做“ 一致相合性” 。
相關定理
定義
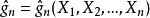 相合性
相合性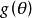 相合性
相合性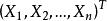 相合性
相合性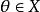 相合性
相合性 相合性
相合性定義1 設為的基於樣本的的一個估計量,若對任意固定的,都滿足:對於任給的,有
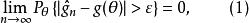 相合性
相合性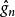 相合性
相合性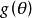 相合性
相合性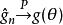 相合性
相合性成立,則稱為的 相合估計,上述極限式簡記為。
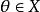 相合性
相合性定義2若對任何固定的都有
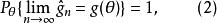 相合性
相合性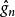 相合性
相合性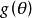 相合性
相合性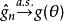 相合性
相合性則稱為的 強相合估計量,上述式子可簡記為,這裡a.s.為almost surely的縮寫。
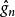 相合性
相合性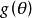 相合性
相合性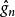 相合性
相合性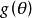 相合性
相合性式(1)表明隨機變數序列 依機率收斂於,而式(2)即 幾乎處處收斂於。由以上定義以及幾乎處處收斂和依機率收斂之間的關係知, 強相合估計必為相合估計。
定理1
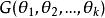 相合性
相合性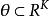 相合性
相合性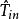 相合性
相合性 相合性
相合性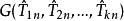 相合性
相合性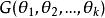 相合性
相合性設在參數空間上連續,為的強相合估計量,i=1,2,...,k,則為的強相合估計量。
定理2
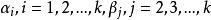 相合性
相合性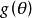 相合性
相合性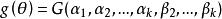 相合性
相合性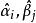 相合性
相合性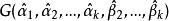 相合性
相合性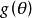 相合性
相合性設總體有直到k(k≥2)階的矩。可表示為,且G為連續函式。記分別為樣本原點矩和樣本中心矩,則為的強相合估計量。
注意:由該定理可知,矩估計量一般是強相合的。
定理3
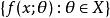 相合性
相合性設分布族滿足:
(1)X是有限集;
(2)對於不同的參數值θ和θ’,所對應的分布不同;
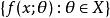 相合性
相合性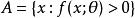 相合性
相合性(3)有共同支撐,即與θ無關;
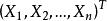 相合性
相合性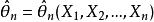 相合性
相合性 相合性
相合性則對於簡單隨機樣本,θ的最大似然估計量存在,且為θ的相合估計量。
定理4
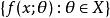 相合性
相合性設分布族滿足:
(1)θ為R(一維實空間)中的開集;
(2)不同的參數值θ和θ’,所對應的分布不同;
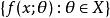 相合性
相合性(3)有共同支撐A;
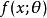 相合性
相合性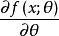 相合性
相合性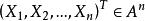 相合性
相合性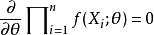 相合性
相合性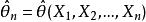 相合性
相合性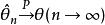 相合性
相合性 相合性
相合性(4)對θ的偏導數在X上存在,並且當簡單隨機樣本時,似然方程有且僅有解,則,即為θ的相合估計量。
例題解析
例1
 相合性
相合性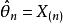 相合性
相合性設,則是θ的有偏估計,但它是相合的。
證明:
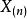 相合性
相合性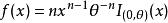 相合性
相合性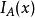 相合性
相合性的密度函式為,此處為A的示性函式。故對任意ε>0,有
 相合性
相合性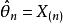 相合性
相合性可見為θ的相合估計。
例2
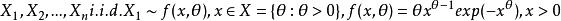 相合性
相合性設,證明θ的極大似然估計是相合的。
證明:似然函式為
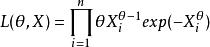 相合性
相合性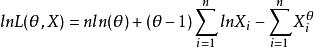 相合性
相合性故有
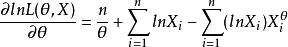 相合性
相合性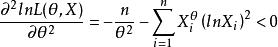 相合性
相合性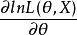 相合性
相合性可見為θ的嚴格單調下降函式。又因為
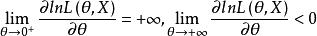 相合性
相合性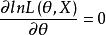 相合性
相合性從而有且僅有一個解。故似然方程的根必為極大似然估計量且是相合估計。