基本介紹
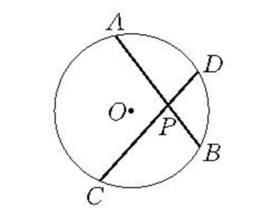
相交弦是圓內相關的兩條弦。在圓的內部相交的兩條弦，稱為相交弦。如圖1，弦AB和CD相交於⊙O內一點P，則AB和CD為⊙O的相交弦。
相交弦定理及其推論
相交弦定理
相交弦定理 圓內的兩條相交弦，被交點分成的兩條線段長的積相等。
相交弦定理還可以敘述為“圓的弦相交於圓內的一點，各弦被這點內分成的兩線段長的乘積相等”。
如圖1，⊙O中兩弦AB、CD相交於點P，則AP·PB=CP·PD。
相交弦定理揭示了圓內兩條相交的弦的性質，即各弦被交點分成的兩條線段長的積相等。這個定理在解決圓中證明及計算問題時經常用到。
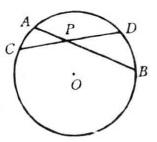圖1【例1】圓內有相交兩弦，一弦長為8cm，並被交點平分，另一弦被交點分成1 :4兩部分，求另一弦的長。
解: 設另一弦被交點分成的兩部分的長分別為a和4a。
依據相交弦定理，得a·4a=4。
解得 a=±2 (舍負)。
所以另一弦的長為(a+4a)=5a=5×2=10(cm)。
【例2】如圖2，已知:弦AB、CD相交於點P，且P是AB的中點，若PC=4，PD=9，求AB的長。
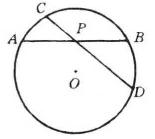圖2解: 因為AB、CD相交於P，
所以PA·PB=PC·PD。
因為P是AB的中點，
所以PA=PB。
因為PC=4，PD=9，
所以PA=4×9= 36。
所以PA=6。
所以AB=2PA= 12。
相交弦定理的推論
相交弦定理的推論如果弦與直徑垂直相交，那么弦的一半是它分直徑所成的兩條線段的比例中項。若a:b=b:c, 則稱b為a、c的比例中項。這個推論揭示了弦與直徑垂直相交的性質。推論在解題中有較廣泛的套用，並給出了作兩條已知線段比例中項的方法。
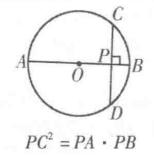圖3相交弦定理的推論