基本介紹
基本概念
直三面角是一種特殊的三面角,三面角的二面角有直角時,按直二面角是一個、兩個或三個,分別稱為單直三面角、雙直三面角和三直三面角。通常三直三面角簡稱直三面角(下文的直三面角指的是三直三面角),直三面角的三個面角也都是直角,直三面角從以頂點為球心的球面截下的球面三角形的三個內角都是直角,其面積是球面面積的八分之一。直多面角亦稱直多面體角,是一種特殊的多面角,指以多面角的頂點為球心作單位球面,如果多面角在單位球面上截出的部分(球面多面形)的面積等於全球面面積的八分之一(即π/2),則稱該多面角為直多面角 。
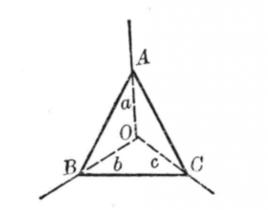
例如,在圖1中,由S,以及SA、SB、SC和相鄰射線組成的面,組成的三面角,且每個面角都是直角,因此,三面角S-ABC是直三面角。一般房間的一個牆角是直三面角 。
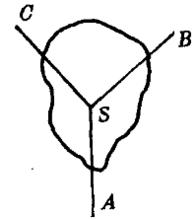 圖1
圖1定理
直三面角的各個二面角都是直二面角。
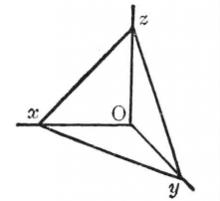 圖2
圖2證明 設直三面角O-xyz。
∵∠xOy=∠yOz=∠zOx=90°,
∴Oz⊥Ox,Oz⊥Oy,
∴∠xOy是二面角x-Oz-y的平面角。
∵∠xOy=90°,
∴二面角x-Oz-y是直二面角。
同理 z-Ox-y、x-Oy-z都是直二面角。
例題解析
【例1】三面角的三個二面角的平分面,相交於同一條直線。
已知 三面角P-ABC。
求證 三個二面角 PA、PB、PC的平分面相交於一直線。
證明 設二面角PA和二面角PB的平分面相交於直線PO,
∵ PO在二面角PA的平分面內,
∴PO上的點至平面PAB和平面PAC的距離相等,
∵PO在二面角PB的平分面內,
∴PO上的點至平面PAB和平面PBC的距離相等,
∴PO上的點至平面PAC和平面PBC的距離相等,
∴PO必在平面PAC和平面PBC所組成的二面角PC的平分面內,
∴ 三個二面角的平分面相交於直線PO。
從本題可知:“至三面角的三個面距離相等的點的軌跡,是這三面角的三個二面角的平分面的交線。”
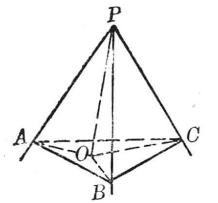 圖3
圖3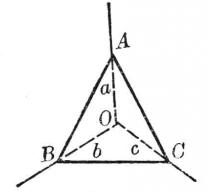 圖4
圖4【例2】如果一個平面截直三面角,則截面是一個銳角三角形。
已知 直三面角O-ABC,平面ABC截它交三條棱OA、OB、OC分別於A、B、C。
求證 截面△ABC為銳角三角形。
證明 令OA=a,OB=b,OC=c,
∵O-ABC是直三面角,
∴它的三條棱兩兩互相垂直,
∴AB²=a²+b²,AC²=a²+c²,BC²= b²+c²,
∴AB²+ AC²=2a²+b²+c²>b²+c²= BC²。
同理 AB²+ BC²>AC²,AC²+BC²>AB²。
因為“一個三角形如果任意兩條邊的平方和大於第三條邊的平方,則這個三角形是銳角三角形”。
∴△ABC為銳角三角形。
【例3】一個平面截直三面角,則截面銳角三角形的垂心,是頂點在截面上的射影。
已知 直三面角O-ABC,平面ABC分別截三條棱OA、OB及OC於A、B、C,G為截面△ABC的垂心。
求證 G為頂點O在△ABC上的射影。
證明 ∵G為△ABC的垂心,
∴連線AG引長交BC於D,則AD⊥BC,
∴AO⊥BO,AO⊥CO,
∴AO⊥平面BOC,AO⊥BC,
∴BC⊥平面AOD,
∴平面AOD⊥平面ABC。
同理 連線CG引長交AB於E,連線EO,則平面COE⊥平面ABC。
∴平面AOD和平面COE的交線OG垂直於平面ABC,
∴點G是頂點O在△ABC所在平面的射影。
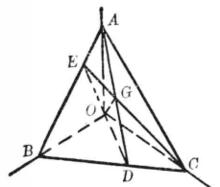 圖5
圖5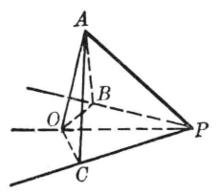 圖6
圖6說明 當截面△ABC位置給定以後,由於△ABC的垂心G是唯一的,頂點O在△ABC所在平面的射影也是唯一的,所以這個命題的條件和結論都具有唯一性,故可運用同一法去證明它的等效命題“一個平面截直三面角,則頂點在截面上的射影,是截面銳角三角形的垂心” 。