定義
誠然,正如局域化分子軌道,瓦尼爾函式也有許多選取的方式,但最原始的,最簡單的,且最常見的定義如下:
選定晶體中的某單一能帶,將其布洛赫態標記為
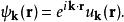 瓦尼爾函式
瓦尼爾函式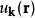 瓦尼爾函式
瓦尼爾函式其中 的周期性和晶體的相同。於是瓦尼爾函式就被定義為
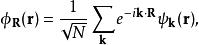 瓦尼爾函式
瓦尼爾函式•R表示任意格矢(即對於每一布拉維格矢都有一與其對應的瓦尼爾函式);
•N為晶格中原胞的數量;
•對k的求和包含布里淵區(或倒易點陣中滿足周期性邊界條件的原胞)中的N個不同的k,均勻地分布在整個布里淵區內。由於{\displaystyle N}的值通常較大,為了簡化運算會使用如下關係來把此求和化為積分:
•其中的“BZ”表示布里淵區,其體積為Ω。
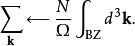 瓦尼爾函式
瓦尼爾函式現代的極化理論
最近的研究將瓦尼爾函式套用到描述晶體中的極化現象中,例如鐵電性。電極化的現代理論解釋是由Raffaele Resta和David Vanderbilt提出的, 參見Berghold,和Nakhmanson所發表的文章,以及Vanderbilt的介紹。固體中每一單位晶胞的極化強度可被定義為瓦尼爾電荷密度的電偶極矩:
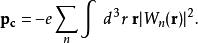 瓦尼爾函式
瓦尼爾函式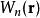 瓦尼爾函式
瓦尼爾函式其中的求和符號是對所有占據能帶的求和,指的是對於能帶 n 局域於晶胞中的瓦尼爾函式。在連續的物理過程中,極化強度的變化即為極化的時間導數,可用布洛赫占有態的貝里相位確切地闡述。
參見
•軌道磁化
•布洛赫波
•Hannay角
•幾何相位
