公式
設所求點A緯度角β1,經度角α1, 點B 緯度角β2, 經度角α2
=R·arc cos[cosβ1cosβ2cos(α1-α2)+sinβ1sinβ2] (I)上述公式推導中只需寫出A,B兩點的球面坐標,運 用向量的夾角公式、弧長公式就能得出結論,簡單明了,易於理解,公式特徵明顯·從公式的推導中我們體會到坐標法在解決立幾問題的不凡表現。
由公式(I)知,求地球上兩點的球面距離,不需求弦AB,只需兩點的經緯度即可。
公式對求地球上任意兩點球面距離都適用,特別地,A、B兩點的經度或緯度相同時,有:
1、β1=β2=β,則球面距離公式為:
=R·arcos[cosβcosβcos(α1-α2)+sinβsinβ] (II)
2、α1=α2=α,則球面距離公式為:
=R·arcos(cosβ1cosβ2+sinβ1sinβ2)=R·arcoscos(β1-β2) (III)
例1、 北緯45º的緯線上,A、B兩點的球面距離是 R,A在東經20º,求B點的位置。
分析:α1=20º,β1=β2=45º,由公式(II)得:
R= R·arcos[cos45ºcos(20º-α2)+sin45º]
cos = cos(20º-α2)+
∴cos(20º-α2)=0, 20º-α2=±90º即:α2=110º或α2=-70º
所以B點在北緯45º,東經110º或西經70º
提出問題
已知球面的兩點,為了方便起見,以經緯度來唯一標識點的位置(相關概念請參照2.相關預備知識),要求計算出它們的球面距離。
相關知識
這兒提到的預備知識是地球的相關知識,如形狀和大小、緯度和經度等相關概念。
(1)形狀和大小:
地球形狀是一個兩極部位略扁的不規則的球體。地球的平均半徑為6371千米,赤道半徑6378千米,極半徑6357千米。赤道周長約為4萬千米。
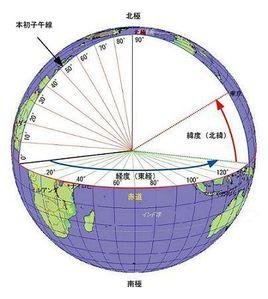
(2)緯線和緯度、經線和經度
①緯線:緯線都是圓,也稱為緯線圈,長度不等。赤道最長,由赤道向兩極逐漸縮短,最後成一點。緯線指示東西方向。
② 緯度:地球上任意一點與地心的連線和赤道面所形成夾角的度數即為此點所在緯線的緯度。赤道是零度緯線。赤道以北的緯度,叫北緯,用“N”作代號;赤道以南的緯度叫南緯,用“S”作代號。北緯、南緯各有90°。
③ 經線:也叫子午線。經線是半圓,所有經線長相等。經線指示南北方向。
④ 經度:每條經線(子午線)與地軸所形成的平面和本初子午線與地軸所形成平面夾的二面角的角度即為此條經線的經度。零度經線叫做本初子午線。從本初子午線向東、向西各分作180度,以東的180°屬於東經,用“E”作代號;以西的180°屬於西經,用“W”作代號。
例題
東西180°經線合為一條經線。
用20°W和160°E的經線圈,將地球分為東、西兩個半球。
如上圖,先假設球的半徑為R,所給定的2點為A,B兩點,先假設A在北半球,B在南半球。這只是其中的一種情況,至於其它的情況可以同樣的方法計算出,僅僅是大同小異而已。當然,還有特殊情況也不能忘了喔。
假設球心為點O,那么最後得到的∠AOB的弧度乘以球的半徑R即為所求的球面距離。
設經過球的南極和北極的極點的直線為l,分別過點B、A作l的垂線,設垂點分別為D、C。
過點作線BC的平行線,過B作CD的平行線,這兩條平行線必定相交,設交點為E,容易證明BDCE是一個矩形。
由於A、B點的經緯度已知,所以∠OBD和∠OAC也已知,設分別為β,α,由於半徑R已知,所以|BD| = R * cosβ,|AC| = R * cosα,|OD| = R * sinβ,|OC| = R * sinα。
由於點A、B的經度已知,所以不難求出∠ACE的值。所以三角形ACE中不難用餘弦定理求出|AE|的值。
在直角三角形ABE中,容易求出AB的值。此時三角形AOB三條邊都已知,所以∠AOB也可以用餘弦定理求出來,這樣AB的球面距離也迎刃而解了。