簡介
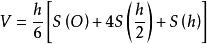牛頓一辛普森公式一個幾何體被垂直於其高（或平行於其底）的平面所截，如果截面面積是它到上底（或下底）的距離的K次函式（K=0,1,2,3），即S(x)=ax +bx +cx+d，則它的體積為 ，式中h為幾何體的高，S(O)，S(h)是上、下底的面積，S(h/2)是中截面面積。
證明
只需要證明根據公式算出來的體積和用積分算出來的體積相等即可。
設截面面積是截面高h的不超過3次的函式：f(h)= ah +bh +ch+d，那么，利用積分計算體積，可以得到（積分限為0~h）：V=∫f(x)dx=ah /4+bh /3+ch /2+dh；利用公式計算體積，可以得到：
V=H(S+4S+S)/6=h(f(0)+4f(h/2)+f(h))/6=h[d+4(ah /8+bh /4+ch/2+d)+(ah +bh +ch+d)]/6
=ah /4+bh /3+ch /2+dh。
因此兩式相等，公式得證。
註：當函式f(h)次數高於或等於4次時，公式一般不成立。這只需驗證f(h)=h 時公式不成立即可。
套用
牛頓-辛普森公式是一種適應面較廣的求積公式。
牛頓-辛普森公式不僅適用於作為擬柱體的稜柱、稜錐和稜台，而且適用於不是擬柱體的圓柱、圓錐、圓台和球檯，甚至像橢球體等。
事實上，其他符合條件（所有頂點都在兩個平行平面上、用平行於底面的平面去截該圖形時所得到的截面面積是該平面與一底之間距離的不超過3次的函式）的立體圖形也可以利用該公式求體積。
