卡諾的研究
 熱機效率
熱機效率法國數學家和工程學家薩迪·卡諾的父親拉札爾·卡諾(Lazre Nico-las Carnot,1753—1823)率先研究了這類問題,在他的著作中討論了各種機械的效率,隱諱地提出這樣一個觀念:設計低劣的機器往往有“丟失”或“浪費”。當時,在水力學中有一條卡諾原理,就是拉札爾·卡諾提出的,說的是效率最大的條件是傳送動力時不出現振動和湍流,這實際上反映了能量守恆的普遍規律。他的研究對他的兒子有深刻影響。
1824年薩迪·卡諾發表了著名論文《關於火的動力及適於發展這一動力的機器的思考》,提出了在熱機理論中有重要地位的卡諾定理,這個定理後來成了熱力學第二定律的先導。他寫道①:
“為了以最普遍的形式來考慮熱產生運動的原理,就必須撇開任何的機構或任何特殊的工作物質來進行考慮,就必須不僅建立蒸汽機原理,而且要建立所有假想的熱機的原理,不論在這種熱機里用的是什麼工作物質,也不論以什麼方法來運轉它們。”
卡諾取最普遍的形式進行研究的方法,充分體現了熱力學的精髓。他撇開一切次要因素,徑直選取一個理想循環,由此建立熱量和其轉移過程中所作功之間的理論聯繫。
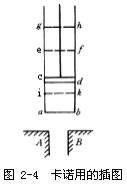
他首先作了如下假設:“構想兩個物體A與B,各保持於恆溫,A的溫度高於B;兩者不論取出熱或獲得熱,均不引起溫度變化,其作用就象是兩個無限大的熱質之庫。我們稱A為熱源,稱B為冷凝器。”如圖2-4。
效率數值
蒸汽機 百分之4~百分之8
蒸汽輪機 百分之25~百分之30
燃氣輪機 百分之50~百分之60
汽油機 百分之26~百分之45
柴油機 百分之34~百分之45
噴氣發動機 百分之50~百分之60
效率數值
蒸汽機 4%~8%
蒸汽輪機 25%~30%
燃氣輪機 50%~60%
汽油機 26%~45%
柴油機 34%~45%
噴氣發動機 50%~60%
彈性流體
然後他構想有一種彈性流體,例如大氣,封閉在裝有活動隔板或活塞cd的圓柱形容器abcd中。
“1.將A與容器 abcd中的空氣或與容器之壁接觸,假設此壁是熱質的良導體。由於這一接觸,空氣得到與A相同的溫度。cd為活塞所處的位置。
“2.活塞逐漸上升,直至取得ef的位置。保持空氣與A接觸,因此在空氣稀釋的過程中溫度保持恆定,物體A提供了保持恆溫所需的熱質。
“3.移開物體A,空氣不再與任何能夠提供熱質的物體接觸,但活塞仍繼續移動,從位置ef達到位置gh,空氣未獲任何熱質而稀釋,它的溫度下降了。假設下降到和物體B的溫度相等,這時活塞停止運動,占有位置gh。
“4.將空氣與物體B接觸,活塞壓縮空氣由位置gh回復到cd。但由於仍與B接觸,空氣保持恆溫,並將熱質交給物體B。
“5.移開物體B,繼續壓縮空氣。由於空氣這時已被隔絕,溫度上升。壓縮一直繼續到空氣達到A的溫度。活塞在此期間從位置cd到了位置ik。
“6.空氣再與 A接觸,活塞從位置ik回到位置 ef,溫度保持不變。
“7.再重新進行(3)中的步驟,以後相繼經4、5、6、3、4、5、6、3、4、5……。”
理想循環
卡諾選取的理想循環是由兩個等溫過程和兩個絕熱過程組成的;等溫膨脹時吸熱,等溫壓縮時放熱,空氣經過一個循環,可以對外作功。
卡諾由這個循環出發,提出了一個普遍的命題:“熱的動力與用於實現動力的工作物質無關;動力的量唯一地取決於熱質在其間轉移的兩物體的溫度。”
卡諾根據熱質守恆的假設和永動機不可能實現的經驗總結,經過邏輯推理,證明他的理想循環獲得了最高的效率。他寫道:“如果有任何一種使用熱的方法,優於我們所使用的,即如有可能用任何一種過程,使熱質比上述操作順序產生更多的動力,那就有可能使動力的一部分轉化於使熱質從物體B送回到物體A,即從冷凝器回到熱源,於是就可以使狀態復原,重新開始第一道操作及其後的步驟,這就不僅造成了永恆運動,甚至還可以無限地創造出動力而不消耗熱質或任何其他工作物質。這樣的創造與公認的思想,與力學定律以及與正常的物理學完全矛盾,因而是不可取的。所以由此可得結論:用蒸汽獲得的最大動力也是用任何其他手段得到的最大動力。”
這就是卡諾定理的最初表述。用現代辭彙來講就是:熱機必須工作在兩個熱源之間,熱機的效率僅僅決定於兩個熱源的溫度差,而與工作物質無關,在兩個固定熱源之間工作的所有熱機,以可逆機效率最高。
不過,由於卡諾信奉熱質說,他的結論包含有不正確的成份。例如:他將蒸汽機比擬為水輪機,熱質比擬為流水,熱質從高溫流向低溫,總量不變。他寫道:“我們可以足夠確切地把熱的動力比之於瀑布。瀑布的動力取決於其高度和液體的量;而熱的動力則取決於所用熱質的量以及熱質的‘下落高度’,即交換熱質的兩物體之間的溫度差。”
卡諾就這樣把熱質的轉移和機械功聯繫了起來。由於他缺乏熱功轉化的思想,因此,對於熱力學第二定律,“他差不多已經探究到問題的底蘊。阻礙他完全解決這個問題的,並不是事實材料的不足,而只是一個先入為主的錯誤理論。”(恩格斯:《自然辯證法》)
卡諾在1832年6月先得了猩紅熱和腦膜炎8月24日又患流行性霍亂去世,年僅36歲。上節所述的他遺留下的手稿表明他後來也轉向了熱的唯動說,並預言了熱功之間的當量關係和熱的分子運動論。可惜,手稿直至1878年才發表,因而對熱學的發展沒有起到應有的作用。
卡諾循環
卡諾效率(Carnot Efficiency) = 1-Tc / Th
Tc 代表卡諾熱機低溫端(環境)的絕對溫度值、Th 代表熱機高溫端工質(氣體)的絕對溫度值;由此計算得知:假如高溫端工質絕對溫度Th在1000K(727℃)、低溫端(環境)絕對溫度Tc在300K(27℃)時,卡諾熱機的最大熱功轉換效率是1-Tc/Th=70%
熱機定律
定義或解釋
轉變為有用功的熱量跟燃料燃燒時放出的熱量的比叫做熱機的效率,也叫熱機的有效效率。通常用百分數來表示。
說明
①凡是能夠利用燃料燃燒時放出的能來做機械功的機器就叫做熱機。
②熱機在工作過程中,發熱器(高溫熱源)里的燃料燃燒時放出的熱量並沒有全部被工作物質(工質)所吸收,而工質從發熱器所得到的那部分熱量也只有一部分轉變為機械功,其餘部分隨工質排出,傳給冷凝器(低溫熱源)。工質所作的機械功中還有一部分因克服機件摩擦而損失。根據熱機的工作特點,下面對熱機中熱量的利用和損耗情況作一說明。
ηC
是指工質從發熱器得到的熱量和燃料燃燒時放出熱量的比。如果用ηC表示,燃料燃燒效率可寫成ηC=Q1/Q。
公式
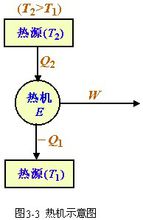
是指熱機工作部分中轉變為機械功的熱量和工質從發熱器得到的熱量的比。如果用ηt表示,則有ηt=W/ Q1=( Q1-Q2) / Q1=1- Q2/ Q1。
從式中很明顯地看出Q1越大,Q2越小,熱效率越高,這是熱機效率中的主要部分,它表明了熱機中熱量的利用程度。
熱機的機械效率是指推動機軸做功所需的熱量和熱機工作過程中轉變為機械功的熱量的比,如果用ηm表示,則有ηm=Q3/(Q1-Q2)等。
熱機效率公式應為η=Q有/Q放×100%
提高效率
熱機的效率是熱機問世以來科學家、發明家和工程師們一直研究的重要問題。現在的內燃機和噴氣機跟最初的蒸汽機相比,效率雖然提高了很多,但從節約能源的要求來看,熱機的效率還遠遠不能滿意。最好的空氣噴氣發動機,在比較理想的情況下其效率也只有60%。用的最廣的內燃機,其效率最多只達到40%。大部分能量被浪費掉了。
1.保證活塞滑動靈活,並且密封性好
2.保證噴頭無損,噴霧均勻
3.連桿轉軸等處摩擦小
4.使用合適的燃料
5.對於不可避免的熱能損失,可以用來加熱水等其他用途