發現理論
1901年, 范霍夫因發現化學動力學定律和滲透壓,提出了化學反應熱力學動態平衡原理,獲第一個諾貝爾化學獎。
 熱力學定律
熱力學定律1906年 能斯特提出了熱力學第三定律,認為通過任何有限個步驟都不可能達到絕對零度。這個理論在生產實踐中得到廣泛套用,因此獲1920年諾貝爾化學獎。
1931年 翁薩格發表論文“不可逆過程的倒數關係”,闡明了關於不可逆反應過程中電壓與熱量之間的關係。對熱力學理論作出了突破性貢獻。這一重要發現放置了20年,後又重新被認識。1968年獲諾貝爾化學獎。
1950年代, 普利戈金提出了著名的耗散結構理論。1977年,他因此獲諾貝爾化學獎。這一理論是當代熱力學理論發展上具有重要意義的大事。它的影響涉及化學、物理、生物學等廣泛領域,為我們理解生命過程等複雜現象提供了新的啟示。
第一定律
實質
能量守恆與轉換定律是自然界的基本規律之一。它指出: 自然界中的一切物質都具有能量, 能量不可能被創造, 也不可能被消滅; 但能量可以從一種形態轉變為另一種形態, 且在能量的轉化過程中能量的總量保持不變。
熱力學第一定律是能量守恆與轉換定律在熱現象中的套用, 它確定了熱力過程中熱力系與外界進行能量交換時, 各種形態能量數量上的守恆關係。
我們知道, 運動是物質的屬性, 能量是物質運動的度量。分子運動學說闡明了熱能是組成物質的分子、原子等微粒的雜亂運動———熱運動的能量。既然熱能和其他形態的能量都是物質的運動, 那么熱能和其他形態的能量可以相互轉換, 並在轉化時能量守恆完全是理所當然的。
在工程熱力學的範圍內, 主要考慮的是熱能和機械能之間的相互轉換與守恆, 所以第一定律可表述為:“熱是能的一種, 機械能變熱能, 或熱能變機械能的時候, 它們間的比值是一定的。” 或“ 熱可以變為功, 功也可變為熱。一定量的熱消失時必產生相應量的功;消耗一定量的功時必出現與之對應的一定量的熱。”
熱力學第一定律是人類在實踐中累積的經驗總結, 它不能用數學或其他的理論來證明, 但第一類永動機迄今仍未造成以及由第一定律所得出的一切推論都與實際經驗相符合等事實, 可以充分說明它的正確性。
基本內容
能量是永恆的,他不會被誰製造出來,也不會被誰消滅。但是熱能可以給動能提供動力,而動能還能夠再轉化成熱能。
普遍的能量轉化和守恆定律在一切涉及熱現象的巨觀過程中的具體表現。熱力學的基本定律之一。
 熱力學定律
熱力學定律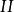 熱力學定律
熱力學定律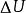 熱力學定律
熱力學定律 熱力學定律
熱力學定律 熱力學定律
熱力學定律表征熱力學系統能量的是內能。通過作功和傳熱,系統與外界交換能量,使內能有所變化。根據普遍的能量守恆定律,系統由初態 經過任意過程到達終態 後,內能的增量 應等於在此過程中外界對系統傳遞的熱量 和系統對外界作功 之差,即
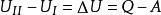 熱力學定律
熱力學定律或
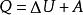 熱力學定律
熱力學定律式中:
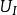 熱力學定律
熱力學定律 熱力學定律
熱力學定律——系統初態 時的能量;
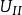 熱力學定律
熱力學定律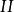 熱力學定律
熱力學定律——系統終態 時的能量;
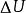 熱力學定律
熱力學定律——系統內能增量;
 熱力學定律
熱力學定律——外界對系統傳遞的熱量;
 熱力學定律
熱力學定律——系統對外界做功差。
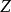 熱力學定律
熱力學定律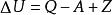 熱力學定律
熱力學定律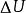 熱力學定律
熱力學定律 熱力學定律
熱力學定律 熱力學定律
熱力學定律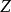 熱力學定律
熱力學定律這就是熱力學第一定律的表達式。如果除作功、傳熱外,還有因物質從外界進入系統而帶入的能量,則應為 當然,上述、、、均可正可負。
微積分表達式
熱力學第一定律的能量方程式就是系統變化過程中的能量平衡方程式, 是分析狀態變化過程的根本方程式。它可以從系統在狀態變化過程中各項能量的變化和它們的總量守恆這一原則推出。把熱力學第一定律的原則套用於系統中的能量變化時可寫成如下形式:
進入系統的能量- 離開系統的能量= 系統中儲存能量的增加
上式是系統能量平衡的基本表達式, 任何系統、任何過程均可據此原則建立其平衡式。對於閉口系統, 進入和離開系統的能量只包括熱量和作功兩項;對於開口系統, 因有物質進出分界面, 所以進入系統的能量和離開系統的能量除以上兩項外, 還有隨同物質帶進、帶出系統的能量。
由於這些區別, 熱力學第一定律套用於不同熱力系統時, 可得不同的能量方程。
對於一個微元過程, 第一定律解析式的微積分形式是:
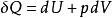 熱力學定律
熱力學定律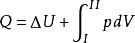 熱力學定律
熱力學定律,
熱力學第一定律的另一種表述是:第一類永動機是不可能造成的。這是許多人幻想製造的能不斷地作功而無需任何燃料和動力的機器,是能夠無中生有、源源不斷提供能量的機器。顯然,第一類永動機違背了能量守恆定律。
第二定律
表述
熱力學第二定律是闡明與熱現象相關的各種過程進行的方向、條件及限度的定律。由於工程實踐中熱現象普遍存在, 熱力學第二定律套用範圍極為廣泛,諸如熱量傳遞、熱功互變、化學反應、燃料燃燒、氣體擴散、混合、分離、溶解、結晶、輻射、生物化學、生命現象、信息理論、低溫物理、氣象以及其他許多領域。
熱力學第二定律的克勞修斯說法:
1850 年, 克勞修斯(Dudolf Clausius)從熱量傳遞方向性的角度提出: 熱不可能自發地、不付代價地從低溫物體傳至高溫物體。
這裡指的是“自發地、不付代價地”。通過熱泵裝置的逆向循環可以將熱量自低溫物體傳向高溫物體, 並不違反熱力學第二定律, 因為它是花了代價而非自發進行的。非自發過程(熱量自低溫傳向高溫) 的進行, 必須同時伴隨一個自發過程(機械能轉變為熱能) 作為代價、補充條件, 後者稱為補償過程。
熱力學第二定律的開爾文說法:
1824 年, 卡諾(Sadi Carnot )最早提出了熱能轉化為機械能的根本條件:“ 凡有溫度差的地方都能產生動力。”實質上, 它是熱力學第二定律的一種表達方式。隨著蒸汽機的出現, 人們在提高熱機效率的研究中認識到, 只有一個熱源的熱動力裝置是無法工作的, 要使熱能連續地轉化為機械能至少需要兩個( 或多於兩個)溫度不同的熱源, 通常以大氣中的空氣或環境溫度下的水作為低溫熱源, 另外還需有高於環境溫度的高溫熱源, 例如高溫煙氣。1851 年左右, 開爾文( LordKelvin)和普朗克(Max Planck) 等人從熱能轉化為機械能的角度先後提出更為嚴密的表述, 被稱為熱力學第二定律的開爾文說法: 不可能製造出從單一熱源吸熱、使之全部轉化為功而不留下其他任何變化的熱力發動機。
方向性
1、 功熱轉化
功可以自動地轉化為熱,功轉熱是不可逆過程, 其反向過程, 即降低流體的熱力學能或收集散給環境的熱量轉化為功重新舉起重物回復原位的過程, 則不能單獨地、自動地進行, 熱不可能全部無條件地轉化為功。
2、熱永遠只能由熱處傳到冷處(在自然狀態下)。
熱量一定自動地從高溫物體傳向低溫物體; 而反向過程, 熱量由低溫傳回高溫、系統回復到原狀的過程,則不能自動進行, 需要依靠外界的幫助。
熵及熵增原理
熵是與熱力學第二定律緊密相關的狀態參數。它是判別實際過程的方向,提供過程能否實現、是否可逆的判據, 在過程不可逆程度的量度、熱力學第二定律的量化等方面有至關重要的作用。
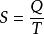 熱力學定律
熱力學定律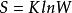 熱力學定律
熱力學定律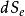 熱力學定律
熱力學定律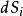 熱力學定律
熱力學定律克勞修斯首次從巨觀角度提出熵概念(),而後波爾茲曼又從微觀角度提出熵概念(),其兩者是相通的,近代的普里戈金提出了耗散結構理論,將熵理論中引進了熵流的概念,闡述了系統內如果流出的熵流()大於熵產生()時,可以導致系統內熵減少,即
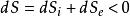 熱力學定律
熱力學定律這種情形應稱為相對熵減。但是,若把系統內外一併考察仍然服從熵增原理。
熵增原理最經典的表述是:“絕熱系統的熵永不減少”,近代人們又把這個表述推廣為“在孤立系統內,任何變化不可能導致熵的減少”。熵增原理如同能量守恆定律一樣,要求每時每刻都成立。關於系統有四種說法,分別叫孤立、封閉、開放和絕熱系統,孤立系統是指那些與外界環境既沒有物質也沒有能量交換的系統,或者是系統內部以及與之有聯繫的外部兩者總和,封閉系統是指那些與外界環境有能量交換,但沒有物質交換的系統,開放系統是指與外界既有能量又有物質交換的系統,而絕熱系統是指既沒有粒子交換也沒有熱能交換,但有非熱能如電能、機械能等的交換。
第三定律
表述
1912 年, 能斯特根據他所提出的熱定理推論, 得出:絕對零度不可能達到。敘述成定律的形式為:“ 不可能套用有限個方法使物系的溫度達到絕對零度。”
上述定律是熱力學第三定律的表述方式之一。絕對零度不可能達到, 看來是自然界中的一個客觀規律。這個規律的本質意義為, 物體分子和原子中和熱能有關的各種運動形態不可能全部被停止。這與量子力學的觀點相符合, 也符合辯證唯物主義的觀點:“ 運動是物質的不可分割的屬性”。任何一種運動形態看來都不可能完全消失。
根據能斯特熱定理推出絕對零度不可能達到的推理如下:據能斯特熱定理,物系在接近絕對零度下進行定溫過程時, 物系的熵不變。物系的熵不變的過程本為孤立系統的可逆絕熱過程。所以, 在接近絕對零度時絕熱過程也具有了定溫的特性, 這時就不可能再依靠絕熱過程來進一步降低物系的溫度以達到絕對零度。
所以, 熱力學第三定律的上述兩種敘述方式是等效的, 其中任何一種都可以從另一種推出。
第二定律告訴我們,得有溫度更低的東西才能使熱量轉移,所以,在絕對零度,你不能讓任何東西變得更冷。
“在絕對零度下任何純粹物質完整晶體的熵等於零”。即
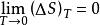 熱力學定律
熱力學定律式中
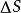 熱力學定律
熱力學定律——熵變化值;
 熱力學定律
熱力學定律——定溫過程。
第零定律
表述
如果兩個熱力學系統中的每一個都與第三個熱力學系統處於熱平衡(溫度相同),則它們彼此也必定處於熱平衡。這一結論稱做“熱力學第零定律”。
熱力學第零定律的重要性在於它給出了溫度的定義和溫度的測量方法。
定律中所說的熱力學系統是指由大量分子、原子組成的物體或物體系。它為建立溫度概念提供了實驗基礎。這個定律反映出:處在同一熱平衡狀態的所有的熱力學系統都具有一個共同的巨觀特徵,這一特徵是由這些互為熱平衡系統的狀態所決定的一個數值相等的狀態函式,這個狀態函式被定義為溫度。而溫度相等是熱平衡之必要的條件。
適用範圍
第零定律是在不考慮引力場作用的情況下得出的,物質(特別是氣體物質)在引力場中會自發產生一定的溫度梯度。如果有封閉兩個容器分別裝有氫氣和氧氣,由於它們的分子量不同,它們在引力場中的溫度梯度也不相同。如果最低處它們之間可交換熱量,溫度達到相同,但由於兩種氣體溫度梯度不同,則在高處溫度就不相同,也即不平衡。因此第零定律不適用引力場存在的情形。這與限定第二類永動機不成立的第二定律類似。
意義
熱力學第零定律用來作為進行體系測量的基本依據,其重要性在於它說明了溫度的定義和溫度的測量方法。表述如下:
1、可以通過使兩個體系相接觸,並觀察這兩個體系的性質是否發生變化而判斷這兩個體系是否已經達到熱平衡。
2、當外界條件不發生變化時,已經達成熱平衡狀態的體系,其內部的溫度是均勻分布的,並具有確定不變的溫度值。
3、一切互為平衡的體系具有相同的溫度,所以一個體系的溫度可以通過另一個與之平衡的體系的溫度來表示,也可以通過第三個體系的溫度來表示。