基本內容
原問題,又稱原線性規劃問題,是指每一個線性規劃的原始問題,每個原問題均可以轉化為與其對稱的對偶問題。對偶問題是指每一個線性規劃問題都伴隨有另一個線性規劃問題。原問題與對偶問題之間是互為對偶的關係。沒有絕對的原問題,也沒有絕對的對偶問題。
用單純形法求解線性規劃問題時,疊代的每一步在得到原問題一個基本可行解的同時,其檢驗數行各變數檢驗數的相反數是其對偶問題的一個基本解;在單純形表中,原問題的鬆弛變數對應對偶問題的變數,對偶問題的剩餘變數對應原問題的變數;這些互相對應的變數如果在一個問題的解中是基變數,則在另一問題的解中是非基變數。
分類
如果一線性規劃問題具有無界解,則其對偶問題具有無可行解;
如果一線性規劃問題具有無可行解,則其對偶問題具有無界解或無可行解。
1.如果一線性規劃問題具有無界解,則其對偶問題具有無可行解;
2.如果一線性規劃問題具有無可行解,則其對偶問題具有無界解或無可行解。
舉例
例:設原問題如下,分析其對偶問題的性質。
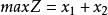 無解性
無解性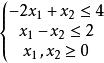 無解性
無解性解析:分析可得線性規劃原問題是無界的,則其對偶問題具有無可行解。
套用
對偶問題在現代數學特別是幾何學、代數學、拓撲學等學科中有著廣泛的套用,對於推動數學的發展起著很好的作用。舉例來講,在運籌學中運用對偶問題的性質,了解線性規劃的無解性內容,明確線性規劃問題具有無界解,則其對偶問題具有無可行解;線性規劃問題具有無可行解,則其對偶問題具有無界解或無可行解等內容,可以有助於更方便快速的解決實際問題,減少計算時間。

