基本介紹
為了使中心射影成為雙射,我們需要改造直線、平面和空間,要求在改造直線和平面的時候滿足下列三個基本關係:
(1)兩條相異的共面直線確定唯一一個點(交點)。
(2)兩個相異點確定唯一一條直線(連線)。
(3)兩個相異平面確定唯一一條直線(交線)。
我們的做法就是給平行直線添加交點。
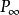 無窮遠元素
無窮遠元素約定: (1)在每一條直線上添加唯一個點,此點不是該直線上原有的點,稱為 無窮遠點(或理想點),記作。在相互平行的直線上添加的無窮遠點相同,不平行的直線上添加的無窮遠點不同 。
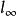 無窮遠元素
無窮遠元素(2)平面上全體無窮遠點構成一條直線,稱為 無窮遠直線(或理想直線),記作。
(3)空間中所有無窮遠點構成的集合構成一平面,稱為 無窮遠平面(或理想平面)。
增加了無窮遠點的直線叫仿射直線,增加了無窮遠直線的平面叫仿射平面,增加了無窮遠平面的空間叫仿射空間。為區別起見,我們稱仿射空間原有的點為有窮遠點或通常點;把除無窮遠直線外的直線稱為有窮遠直線或通常直線;把除無窮遠平面以外的平面稱為有窮遠平面或通常平面。
在平面上添加無窮遠元素之後,沒有破壞點與直線的關聯關係,同時也使得中心射影成為雙射。中心射影也叫透視對應 。
例題解析
例1在仿射空間中,我們有以下命題 :
(1)平面上的每一個方向有唯一的無窮遠點。任意一組平行的直線交於同一無窮遠點;交於同一無窮遠點的直線相互平行。
(2)不平行的直線上的無窮遠點不同。
(3)平面上的平行直線交於無窮遠點,不平行的直線交於通常點,因此平面上任意兩條直線交於唯一一點。
(4)直線或者在某平面上,或者與這個平面交於唯一一點。
(5) 一組平行平面上的無窮遠直線是相同的,這條無窮遠直線就是這組平行平面的交線。
(6)平面上每一條直線(無窮遠直線除外)與無窮遠直線有且僅有一個交點,這個交點就是該直線上的無窮遠點。
(7)每一平面上有且僅有一條無窮遠直線。
(8)空間中任意兩張平面有唯一的交線。兩平行平面的唯一交線是無窮遠直線;兩不平行的平面的唯一交線 是通常直線。
如果把通常點和無窮遠點不加區別;則仿射直線就叫射影直線;仿射平面就叫射影平面;仿射空間叫射影空間 。

