基本介紹
 無環條件
無環條件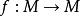 無環條件
無環條件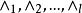 無環條件
無環條件 無環條件
無環條件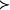 無環條件
無環條件無環條件(no cycle condition)是 穩定性的基本條件之一,描述了動力系統的不變集之間的關係。設M是緊緻流形, 是同胚, 是兩兩不相交的 的閉不變集。在這些集合間定義如下所述的一種關係“ ”:
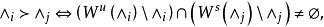 無環條件
無環條件這裡
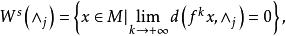 無環條件
無環條件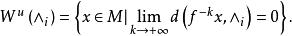 無環條件
無環條件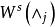 無環條件
無環條件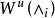 無環條件
無環條件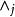 無環條件
無環條件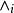 無環條件
無環條件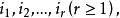 無環條件
無環條件和 分別稱為 的穩定集和 的不穩定集。如果存在兩兩不相同的 使得
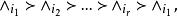 無環條件
無環條件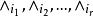 無環條件
無環條件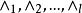 無環條件
無環條件 無環條件
無環條件 無環條件
無環條件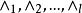 無環條件
無環條件 無環條件
無環條件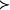 無環條件
無環條件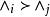 無環條件
無環條件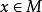 無環條件
無環條件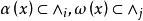 無環條件
無環條件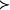 無環條件
無環條件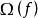 無環條件
無環條件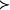 無環條件
無環條件則稱 形成了一個環。如果在 中不存在任何環,則稱關係“ ”是無環的。對M上的連續流 而言,其無環性可如下說明:如果 是兩兩不相交的 的閉不變集,在這些集合間定義如下所述的一種關係“ ”∶ ⇔對某 有 。於是,如上可定義關係“ ”的無環性。通常所說公理A系統滿足 無環條件或具有 無環性質是指: 的譜分解的基本集關於關係“ ”是無環的,即基本集滿足無環條件。在Ω穩定性研究中,無環條件的提出是以Ω爆炸為其背景的。已經證明:滿足公理A和無環條件的系統是Ω穩定和拓撲Ω穩定的,並且Ω穩定蘊涵滿足公理A和無環條件 。
相關概念
基本集
 無環條件
無環條件 無環條件
無環條件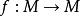 無環條件
無環條件 無環條件
無環條件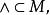 無環條件
無環條件基本集(basic set)是動力系統研究的重要不變集之一,它是根據公理 系統譜分解的基本集所具有的動力學性質而抽象出來的概念。設 是微分流形, 是微分同胚,如果 的一個閉不變集 滿足;
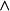 無環條件
無環條件1. 是雙曲的;
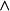 無環條件
無環條件2. 周期點在 中稠密;
 無環條件
無環條件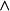 無環條件
無環條件3. 在 上是拓撲傳遞的;
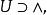 無環條件
無環條件4. 存在開集 使得
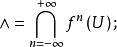 無環條件
無環條件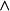 無環條件
無環條件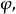 無環條件
無環條件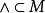 無環條件
無環條件 無環條件
無環條件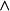 無環條件
無環條件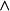 無環條件
無環條件則稱 是基本集,對M上的可微流 設 是 的閉不變集,如果 是一個雙曲奇點,或者 滿足:
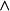 無環條件
無環條件1. 是雙曲的且不含奇點;
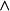 無環條件
無環條件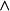 無環條件
無環條件2. 中周期軌道上的點在 中稠密;
 無環條件
無環條件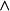 無環條件
無環條件3. 在 上是拓撲傳遞的;
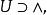 無環條件
無環條件4. 存在開集 使得
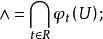 無環條件
無環條件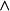 無環條件
無環條件則稱 是基本集,在動力系統的研究中,對基本集的理解一般認為它不是單獨的一個雙曲不動點(雙曲奇點)。基本集的作用在於它在很大程度上確定了系統的軌道結構 。
Ω穩定性
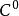 無環條件
無環條件拓撲Ω穩定性(topological Ω-stability)亦稱Ω半穩定性,通常是用來描述系統在小擾動下非遊蕩集的穩定性質的.
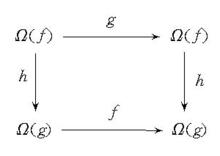 圖1
圖1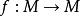 無環條件
無環條件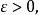 無環條件
無環條件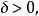 無環條件
無環條件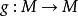 無環條件
無環條件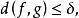 無環條件
無環條件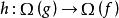 無環條件
無環條件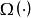 無環條件
無環條件設M是緊緻度量空間,是同胚,如果對任意存在使對任一同胚,只要就存在連續滿射(其中表示( ·)的非遊蕩集),滿足:
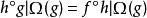 無環條件
無環條件1.,即上圖可交換;
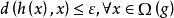 無環條件
無環條件2.;
 無環條件
無環條件 無環條件
無環條件則稱是拓撲穩定的。
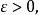 無環條件
無環條件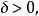 無環條件
無環條件 無環條件
無環條件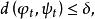 無環條件
無環條件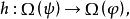 無環條件
無環條件對M上的連續流而言,其定義如下:設φ是M上的連續流,如果對任意存在使得對M上任一連續流ψ,只要對任意有就存在連續滿射滿足:
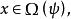 無環條件
無環條件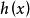 無環條件
無環條件1.對任h將ψ過x的軌道映到φ過的軌道上;
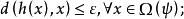 無環條件
無環條件2.
 無環條件
無環條件 無環條件
無環條件則稱φ是拓撲穩定的。公理A和無環條件蘊涵著拓撲穩定性 。

