測地線方程

測地線方程是測地線對應的曲線方程。測地線是線長極短的線，滿足其切矢量沿線平移。

方程形式

抽象指標下某時空的測地線方程形式為：

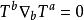測地線方程

其中，

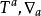測地線方程

分別是測地線的切矢量和該時空的協變導數。

若考慮某一坐標系{xμ}，測地線方程可以寫成分量形式：

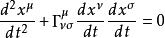測地線方程

其中，

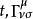測地線方程

分別為測地線的仿射參數和該坐標系下的克氏符。

性質

測地線方程是一個二階微分方程組，由於各未知函式及其一階導數在各個方程中互相耦合，求解並不簡單。但是如果時空有足夠數量的Killing矢量場，那么就可以利用測地線的切矢和Killing矢量場的內積在測地線上為常數的性質把測地線方程化為一階微分方程求解。

套用

通過愛因斯坦場方程確定時空度規後就可以解測地線方程來得到自由粒子的運動軌跡。廣義相對論最初的觀察結果驗證日食的光偏折的理論計算，便是愛因斯坦求解史瓦西時空下的測地線方程，利用其一級近似得出的結論。