泰勒中值定理

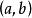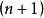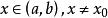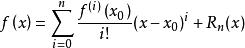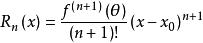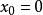泰勒中值定理，是高等數學中的一項定理。

函式介紹

泰勒中值定理

泰勒中值定理

泰勒中值定理

泰勒中值定理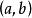

泰勒中值定理

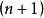泰勒中值定理

泰勒中值定理

泰勒中值定理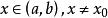

泰勒中值定理

泰勒中值定理

如果函式在含有的某個開區間內具有直到階的導數，且在閉區間上連續，則對任意的，至少存在一點介於與之間，使得階泰勒公式

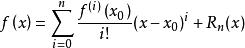泰勒中值定理

成立，

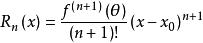泰勒中值定理

泰勒中值定理

其中（拉格朗日型餘項）或（佩亞諾型餘項）。

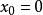泰勒中值定理

當n=0時，即為拉格朗日中值定理；當時，稱為麥克勞林公式。