簡介
在數學中,特別是在運算元理論中, 沃爾德分解或 Wold-von Neumann分解(以Herman Wold和John von Neumann命名)是給定希爾伯特空間上等距線性運算元的分類定理。它指出,每一個等距都是單方面轉變和單一經營者的直接總和。
在時間序列分析中,定理意味著任何平穩的離散時間隨機過程都可以分解為一對不相關的過程,一個是確定性的,另一個是移動平均過程。
細節
讓 H是Hilbert空間, L( H)是對有界運算符 H,和 V∈ L( H)是一個等距。該 沃爾德分解指出,每一個等距 V採用的形式
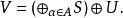 沃爾德分解
沃爾德分解對於一些索引集合 A,其中 S在單方面移上的Hilbert空間 H,和 U是統一的操作(可能空洞)。家庭{ H}由同構希爾伯特空間。
一個證明可以勾畫如下。 V的連續套用給出了 H同構地嵌入自身的下降序列的副本:
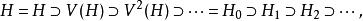 沃爾德分解
沃爾德分解其中 V( H)表示 V的範圍。上面定義的 H= V( H)。如果一個定義
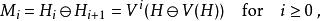 沃爾德分解
沃爾德分解然後
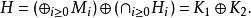 沃爾德分解
沃爾德分解很顯然, K和 K是 V的不變子空間。
所以 V( K)= K。換言之, V限制在 K是一個滿射等距,即, V。
此外,每個 M同構於另一個,其中 V是 M和 M之間的同構: V“移動” M到 M。假設每個 M的維數是某個基數 α。我們看到 K可以寫成直和和Hilbert空間
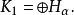 沃爾德分解
沃爾德分解其中每個 H是一個不變子空間 V和 V限制在每個 H是單側移 S。因此
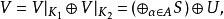 沃爾德分解
沃爾德分解這是一個分解爾德 V 。
備註
從沃爾德分解中立即得出任何適當的,即非單一的等距的光譜是複平面上的單位圓盤。
等距 V被認為是,在上述證明的符號,∩ H= {0}.的 多重性純等距的 V是核心的尺寸 V *,即該指數的基數設定 阿在的爾德分解 V。換句話說,重數 N的純粹等比例形式
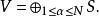 沃爾德分解
沃爾德分解在這個術語中,沃爾德分解表示一個等距作為一個純粹的等距和一個單一的運算元的直接和。
子空間 M被稱為遊蕩子空間的 V如果 V( M) ⊥ V( M)。特別地,上面定義的每個 M是 V的一個漫遊子空間 。
由等軸測圖產生的C * - 代數
考慮等距 V∈ L( H)。通過表示 C *( V)的C * -代數通過生成 V,即 C *( V)是多項式的範數閉合 V和 V *。沃爾德分解可以用來表征 C *( V)。
設 C( T)是單位圓 T上的連續函式。我們記得由單邊移位 S產生的C * - 代數 C *( S)採取以下形式
C*( S) = { T+ K| T是一個Toeplitz運算元與連續符號 f∈ C( T)和 K是一個緊算。
在此識別中, S= T其中 z是 C( T)中的恆等函式。代數 C *( S)被稱為Toeplitz代數。
定理(Coburn) C *( V)與Toeplitz代數是同構的, V是 T的同構圖像。
在Toeplitz代數的描述中,證明取決於與 C( T)的連線,么正運算元的譜包含在圓 T中。
Toeplitz代數的下列性質將是需要的:
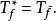 沃爾德分解
沃爾德分解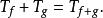 沃爾德分解
沃爾德分解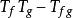 沃爾德分解
沃爾德分解半換法器 是緊湊的。
沃爾德分解說 V是 T的副本的直接和,然後是一個單一的 U:
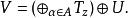 沃爾德分解
沃爾德分解所以我們調用連續泛函微分 f→ f( U),並定義
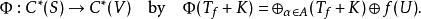 沃爾德分解
沃爾德分解可以驗證Φ是一種將單向偏移映射到 V的同構:
通過上面的性質1,Φ是線性的。地圖Φ是單射因為 T不緊湊對於任何非零 f∈ C( T),並且因此 T+ K= 0意味著 f= 0。由於Φ的範圍是C * -代數,Φ是滿射由 C *( V)的最小值。屬性2和連續函式演算確保Φ保留*操作。最後,半擬合器的性質表明Φ是可乘的。所以定理成立 。
