基本介紹
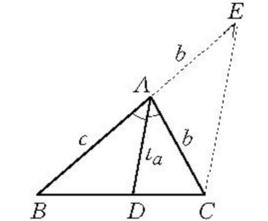
在求線段長度的計算題中，有許多要利用比例線段定理求解．這樣的方法我們稱為比例線段法。例如，已知兩邊b，c及b，c夾角的平分線t，求作三角形。其思路要點是：如圖1，假設△ABC為所求，即AB=c，AC=b，∠A的平分線AD=t，延長BA至E，使AE=b，連結EC，因而AD∥EC，所以利用成比例線段AD/EC=BA/BE，EC=t(b+c)/c，於是△ACE可作出並成為奠基三角形(如圖1)，當t同時大於或等於b，c時，本題無解，否則有一解 。
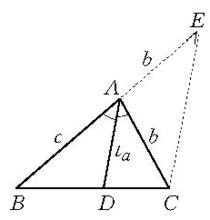圖1例題解析
下面討論將線段比例的性質運用到幾何作圖中去的方法。
首先指出，兩線段的比，根據定義是“用同一長度單位去量兩線段所得的量數之比”。所以四條線段組成的比例實際上是它們四個量數兩兩之比所組成的等量關係。因此，關於數的比例的各個性質，也適用於線段的比例 。
【例1】求作一個三角形與已知三角形相似，且使它的面積等於已知三角形面積的九倍。
已知△ABC，
求作三角形：與△ABC相似，面積是△ABC面積的九倍。
分析設△EFG符合條件: △EFG∽△ABC，S=9S。
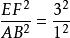比例線段法作圖
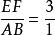比例線段法作圖因為相似三角形面積的比等於對應邊的平方比，設與邊AB對應的邊是EF，則有，所以，EF=3AB。EF可以作出，再根據相似形的性質，可以作出△EFG。
作法 ①作EF =3AB。
②作∠GEF=∠CAB，作∠GFE=∠CBA，EG、FG交於G。
△EFG就是所求作的三角形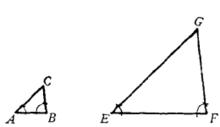，圖2。
圖2證明 ∵∠E=∠A，∠F=∠B (作圖)，
∴ △EFG∽△ABC，
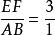比例線段法作圖又：EF= 3AB，即(作圖)，
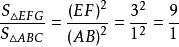比例線段法作圖而(相似形性質及等量代換)，
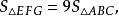比例線段法作圖∴
∴ △EFG符合條件。
討論 僅有一解 。
【例2】已知兩線段的f和，又知它們的比例中項，求作該兩線段。
已知 線段l、f，且I= m+ n，f²= m n，
求作 線段m、n。
分析 考慮到直角三角形中斜邊上的高是斜邊被垂足分成的兩條線段的比例中項，如果將斜邊取成l，高取成f，則被垂足分成的兩條線段就分別是m,n。
作法 ①作AB=l，以AB為直徑畫半圓。
②作直線t // AB 交半圓周於C，且使t與AB間的距離等於f 。
③過C作CD⊥AB交AB於D，
則AD= m，BD =n(或AD=n，BD=m) 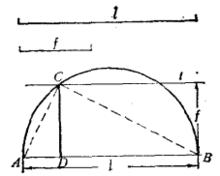(圖3)。
圖3證明 連AC、BC。
∵∠ACB是半圓周上的圓周角，
∴∠ACB= 90°，
∵CD⊥AB (作圖)，
∴CD²= AD BD (直角三角形斜邊上的高是斜邊被垂足分成的兩條線段的比例中項)，
但CD= f (平行線間的距離處處相等)，
∴AD BD=f²，
又 AD+BD= AB=l(作圖)，
AD= m，BD=n(或AD=n、BD= m)。
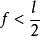比例線段法作圖
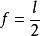比例線段法作圖
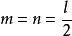比例線段法作圖
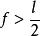比例線段法作圖討論 問題之有解無解取決於t與半圓周交點存在與否。如果，，有兩個交點，有二解，這時m≠n；如果，有切點，這時，一解；如果，t與半圓周無交點，又不相切，無解 。
