基本介紹
解作圖題時,往往首先歸納為求出某一線段長,而這一線段長的表達式能用代數方法求出,然後根據線段長的表達式設計作圖步驟,用這種方法解作圖題,稱為 代數法作圖。
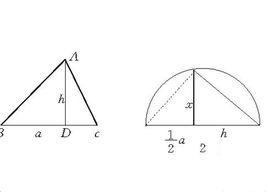
例如,求作一個正方形,使其面積等於已知△ABC的面積,該作圖的思路要點是:設△ABC的底邊為a,高為h(圖1),此題關鍵在於求出正方形的邊長x,由題意,x²=a/2·h,所以x是a/2與h的比例中項(圖2),於是,x可由代數基本作圖法做出,從而符合條件的正方形可以做出 。
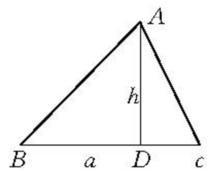 圖1
圖1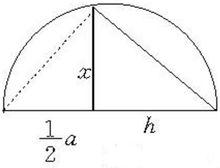 圖2
圖2代數法解作圖題的步驟
用代數手段求出某線段以解作圖題的方法,叫做代數作圖法。
代數法作圖一般有下列幾個步驟,
(1) 以字母表示某些已知的及未知的(欲求的)的量;
(2) 根據條件及已知定理,把已知量和未知量間的關係列成方程(或方程組);
(3) 解此方程(或方程組),求得用已知量表示未知量的解析式;
(4) 根據解析式,利用基本作圖,按步作出圖形 。
常見表達式的形式
在許多作圖題里,要套用代數方法,以x,y,z,...表示未知線段;以a,b,c,...表示已知線段,根據題設的條件,或已知的定理列出方程,並解方程得到它的解,凡求得方程的根為以下形式的,都可以利用基本作圖法作出該未知線段。
(1)x=a+b,;(已知線段和)
(2)x=a-b(a> b);(已知線段差)
(3)x=ma(m為正整數);(已知線段的倍量)
(4)x=a/m(m為正整數)將am等分其中的一分就是x;(已知線段的分量)
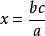 代數法作圖
代數法作圖(5) 即a:b=c:x;即求a,b,c的第四比例項
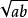 代數法作圖
代數法作圖(6)x=。即求a,b的比例中項
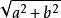 代數法作圖
代數法作圖(7)x=,即作一個以a, b為直角邊的直角三角形,它的斜邊就是x;
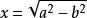 代數法作圖
代數法作圖(8),即作一個以a為斜邊,以b為直角邊的三角形,它的另一條直角邊就是x。
例題解析
【例1】在△ABC中作一內接正方形.
已知:△ABC。
求作:內接正方形DEFG。
分析:如圖3。
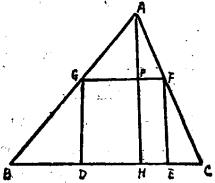 圖3
圖3設 DEFG為所求作的正方形,EF=x,AH⊥BC,AH=h,BC=a 。
根據相似三角形的關係有,
a:x=h:(h~x),
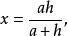 代數法作圖
代數法作圖∴
∵x可以作出,
∴正方形DEFG亦可作出。
作法:
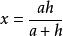 代數法作圖
代數法作圖(1)作線段。
(2)作BC的平行線使它與BC的跑離為x,交AB、AC於G、F。
(3)過G、F作GD⊥BC、EF⊥BC,
則DEFG為所求之內接正方形。
證明: 由作法知GD⊥BC、EF⊥BC,
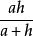 代數法作圖
代數法作圖且GD= EF=,
∴DEFG為矩形。
∵GF//BC,
則BC:GF= AH:(AH-PH),
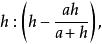 代數法作圖
代數法作圖a:GF =
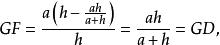 代數法作圖
代數法作圖∴
故DEFG為所求之內接正方形。
討論:因為x可作,所以DEFG亦可作 。
(1)三角形為銳角三角形時,有三解(正方形一邊分別落在a、b、c三邊上)。
(2)三角形為直角三角形時,兩解(正方形的邊落在直角邊時,只有一解;在斜邊上又有一解);
(3)三角形為鈍角三角形時,只有一解(正方形一邊只能落在鈍角所對的邊上)。
注意:代數法作圖的關鍵是求出未知線段的表達式,且這個表達式能用幾何方法作圖。
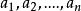 代數法作圖
代數法作圖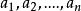 代數法作圖
代數法作圖已知線段,若解析式x =f()運算的結果是單位線段a的一次齊次式,且其中僅有有限次加,減、乘、除、開平方五種運算,則此式對應的線段可用幾何方法作圖。
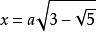 代數法作圖
代數法作圖如,作線段(a為已知線段)。
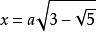 代數法作圖
代數法作圖分析:只要將原式化為
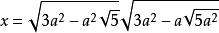 代數法作圖
代數法作圖的形狀即可作出圖形。
凡是A是已知線段的零次齊次式,B是已知線段的一次齊次式,C是已知線段的二次齊次式,並且它們僅含有有限次加、減、秉、除、開平方五種運算,則當方程Ax +Bx+C= 0的根為實數值時,這根的表達式是可作線段。
在代數法作圖時,凡是求作的線段符合.上述兩種情況,定能作出圖形 。