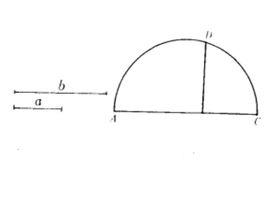
基本介紹
問題“作已知兩條線段的比例中項”相等於問題“作一個正方形，使其面積等於已知矩形的面積?”作已知兩條線段的比例中項的方法很多，其中常用的方法就是根據相交弦定理推論和切割線定理完成的。
註：當矩形的面積和正方形的面積相等時，正方形的邊長是已知矩形兩鄰邊的比例中項。
以下作圖將“作已知兩條線段的比例中項”問題化為“作一個正方形，使其面積等於已知矩形的面積”，其本質是一樣的。“已知兩條線段”即長方形的長和寬，做出來的正方形的邊長即為已知兩條線段的比例中項 。
作圖方法
作法一
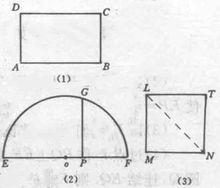圖1作法一：
(1)作線段EP=AB；
(2)延長EP到F，使PF= BC；
(3)以EF為直徑作半圓；
(4)過點P作PG⊥EF，交半圓於點G；
(5)以GP為邊長作正方形LMNT。
GP就是作已知兩條線段的比例中項，正方形LMNT就是所求的正方形。
這個求已知兩線段的比例中項的作圖是根據相交弦定理的推論，容易證明上述作法得出的正方形LMNT的面積與已知矩形的面積相等 。
作法二
設矩形ABCD的AB=a，BC=b，正方形LMNT的邊長為x，則有第二種作法:見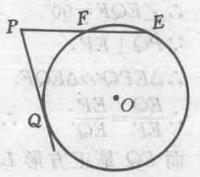圖2。
圖2作法二：
(1)作線段PE，使PE=a；
(2)線上段PE上截取PF，使PF=b；
(3)過E、F兩點任作⊙O；
(4)過點P作⊙O的切線 PQ，切點是Q；
(5)作正方形LMNT，使LM= MN=NT=TL= PQ。
則PQ就是線段a、b的比例中項，正方形LMNT，就是所求的正方形。
容易看出正方形的邊長等於PQ=x，而線段PQ就是矩形的兩鄰邊的長a，b的比例中項，根據就是切割線定理 。
作法三
作法三：
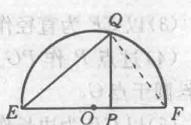圖3(1)作線段EF=a，如圖3所示；
(2)線上段EF上截取EP，使EP=b；
(3)以EF為直徑作半圓；
(4)過點P作PQ⊥EF交半圓Q。連結EQ。則EQ就是線段a、b的比例中項。
(5)以EQ為邊長作正方形LMNT，則LMNT就是所求的正方形。
證明：連結FQ。
∵EF是半圓直徑，
∴∠EQF=90°，
∵PQ⊥EF，
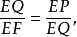比例中項作圖∴
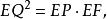比例中項作圖∴
則EQ就是線段a、b的比例中項，EQ是正方形LMNT的邊長，EP、EF是已知矩形ABCD的邊長，因此正方形LMNT的面積等於矩形ABCD的面積 。
