簡介
加權殘差法是一種利用計算機求工程問題微分方程式近似解法數值方法。 加權殘差法又名加權殘值法或加權殘數法,常用於求解微分方程的近似解,具有簡單、精確、迅速、電腦程式短的特點。
原理
若某一問題的基本微分方程及邊界條件可一般地表達為:
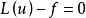 加權殘差法
加權殘差法(u∈Ω) (1.1a)
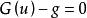 加權殘差法
加權殘差法(u∈Γ) (1.1b)
 加權殘差法
加權殘差法 加權殘差法
加權殘差法式中,L、G表示微分運算元;u為待求變數; 、 為已知函式。
設方程(1.1)的近似解函式為:
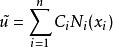 加權殘差法
加權殘差法(1.2)
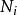 加權殘差法
加權殘差法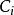 加權殘差法
加權殘差法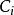 加權殘差法
加權殘差法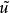 加權殘差法
加權殘差法式中 為給定的試函式; 為待定係數。問題在於選取 使得 逼近真實解u。
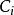 加權殘差法
加權殘差法加權殘差法確定 的原則在於使方程及邊界條件的殘數
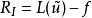 加權殘差法
加權殘差法(1.3a)
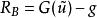 加權殘差法
加權殘差法(1.3b)
加權積分為零,也即在權平均的意義上滿足基本方程與邊界條件,由此可得:
∫RWdΩ = 0 (1.4a)
∫RWdΓ = 0 (1.4b)
或統一表達為:
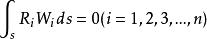 加權殘差法
加權殘差法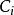 加權殘差法
加權殘差法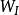 加權殘差法
加權殘差法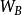 加權殘差法
加權殘差法從而給出關於 的代數方程組,得到問題的近似解。(其中 、 分別是域內、邊界權函式)
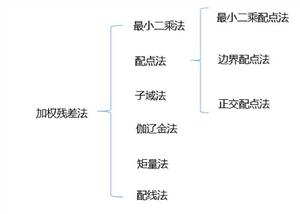
分類
按照權函式的不同形式,加權殘差法主要有以下六種基本類型:
1)最小二乘法
此法較為煩瑣,但所得精度較高。
2)配點法
加權殘差法中最為簡單法一種,在怎樣配點及怎樣處理點值的方法方面又發展出:
I.最小二乘配點法
II.邊界配點法
III.正交配點法
3)子域法
優點在於可將被研究對象分割為有限個區域。
4)伽遼金法
5)矩量法
此法較最小二乘法及伽遼金法為簡便,精度也較配點法及子域法為好。
6)配線法
配點法是在內域或邊界取一些點,使殘數在這些點的值為零。配線法是對配點法的改進,取一些域上的曲線,使殘數在這些曲線的積分值為零。
優點
1)原理統一性
2)不依賴於變分原理,即使泛函不存在也能解題
3)計算誤差可知,殘差即誤差
4)計算方法簡捷高效、準確通用、工作量少及程式簡單
套用
加權殘差法作為一種能夠有效求出微分方程的近似解的數學方法,在國外已發展用於解算流體力學、熱傳導、擴散、對流等非機構問題;在國內,發展用於解算固體力學結構靜、動強度及穩定性問題等,並結合計算機套用,卓有成效地解決了很多計算力學及工程力學的問題。