基本概念
由兩個具有公共底面，且頂點分別在公共底面的兩側的稜錐組成的多面體叫做雙稜錐。
正雙稜錐是一種特殊的雙稜錐，是由兩個有公共底面，頂點分別在公共底面的兩側，且相等的正稜錐組成的多面體。
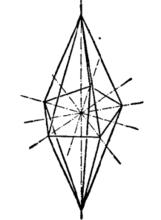圖1 正雙稜錐 n=5相關性質
（1）雙n稜錐是把兩個面變為象點的n稜柱：如果n稜柱有n+2個面，那么雙n稜錐就有n+2個頂點；如果稜柱有2n個頂點，那么它的雙n稜錐就有2n個面。雙n邊形的棱數也一樣。正八面體是雙稜錐最簡單的例子 。
（2）一個直稜柱及個一斜稜柱的容積相等，底面相同，則直稜柱的表面積較小。
正稜錐及一斜棱椎的容積相等，底面相同，正稜錐的表面積較小。
一個正雙稜錐及一個斜雙稜錐的容積相等，底面相同，則正雙稜錐的表面積較小。
（3）正稜錐亦稱正角錐，是一種特殊的稜錐，底面是正多邊形，且頂點在底面的正射影是底面正多邊形的中心的稜錐，正稜錐的頂點與底面中心的連線稱為它的軸，正稜錐是鏡面自對稱的，它的軸是諸對稱鏡面的交線，不是正稜錐的稜錐稱為斜稜錐。正稜錐的主要性質有：
1.各側面都是全等的等腰三角形。
2.各對角面是等腰三角形。
3.各側棱都相等，且側棱在底面上的射影是底面多邊形外接圓的半徑，並平分底面多邊形的一個內角。
4.各斜高都相等，且斜高在底面上的射影是底面多邊形內切圓的半徑，並垂直平分底面多邊形的一條邊。
5.各側面與底面所組成的二面角都相等。
6.各側棱與底面的夾角都相等。
7.相鄰兩個側面所組成的二面角都相等。
8.正稜錐頂點處的多面角是正多面角。
（4）記F為多面體的面數，多面體的面角之和為Σα，多面體的頂點數為V，則有以下表格 ：
| 多面體 | F | Σα | V | 2πV |
| 立方體 | 6 | 12π | 8 | 16π |
| 四面體 | 4 | 4π | 4 | 8π |
| 八面體 | 8 | 8π | 6 | 12π |
| 五稜柱 | 7 | 16π | 10 | 20π |
| 塔 | 9 | 14π | 9 | 18π |
| 十二面體 | 12 | 36π | 20 | 40π |
| 二十面體 | 20 | 20π | 12 | 24π |
| n稜柱 | n+2 | (4n-4)π | 2n | 4nπ |
| n稜錐 | n+1 | (2n-2)π | n+1 | (2n+2)π |
| 雙n稜錐 | 2n | 2nπ | n+2 | (2n+4)π |
根據數據結論可推導出結論：
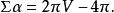正雙稜錐