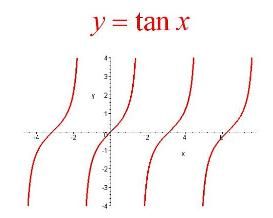基本介紹
正切函式是三角函式的一種英文:tangent
簡寫:tan (也曾簡寫為tg, 現已停用,
中文:正切
概念
如圖,把∠A的對邊與∠A的鄰邊的比叫做∠A的正切,
記作 tan=∠A的對邊/∠A的鄰邊=a/b
銳角三角函式
tan15°=2-√3
tan30°=√3/3
tan45°=1
tan60°=√3
定義
正切函式是直角三角形中,對邊與鄰邊的比值叫做正切。放在直角坐標系中
Tan 取某個角並返回直角三角形兩個直角邊的比值。此比值是直角三角形中該角的對邊長度與鄰邊長度之比,也可寫作tg。
正切tangent,因此在20世紀90年代以前正切函式是用tgθ來表示的,而20世紀90年代以後用tanθ來表示。
將角度乘以 π/180 即可轉換為弧度,將弧度乘以 180/π 即可轉換為角度。
在三角函式中:tanθ=sinθ/cosθ; tanθ=1/cotθ.
在Rt△ABC,∠C=90度,AB=c,BC=a,AC=b,tanA=BC/AC=a/b
將一個角放入直角坐標系中
使角的始邊與X軸的非負半軸重合
在角的終邊上找一點A(x,y)
過A做X軸的垂線
則r=(x^2+y^2)^(1/2)
tan =y/x
性質
1、定義域:{x|x≠(π/2)+kπ,k∈Z}
2、值域:實數集R
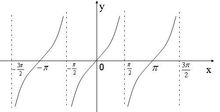 正切函式
正切函式3、奇偶性:奇函式
4、單調性:在區間(-π/2+kπ,π/2+kπ),(k∈Z)上是增函式
5、周期性:最小正周期π(可用T=π/|ω|來求)
6、最值:無最大值與最小值
7、零點:kπ,k∈Z
8、對稱性:
軸對稱:無對稱軸
中心對稱:關於點(kπ/2,0)對稱 (k∈Z)
9、奇偶性:由tan(-x)=-tan(x),知正切函式是奇函式,它的圖象關於原點呈中心對稱
10、圖像(如圖所示)
實際上,正切曲線除了原點是它的對稱中心以外,所有x=(n/2)π點都是它的對稱中心.
誘導公式
tan(2π+α)=tanα
tan(-α) =-tanα
tan(2π-α)=-tanα
tan(π-α) =-tanα
tan(π+α) =tanα
tan(α+β) =(tanα+tanβ)/(1-tanα×tanβ)
tan(α-β) =(tanα-tanβ)/(1+tanα×tanβ)
tan(π/2+α)=-cotα
tan(π/2-α)=cotα