概念
具有正交性並已歸一化的函式叫做“正交歸一化函式”。在量子力學中總是選取正交歸一化函式作為力學量的本徵函式。
量子力學中有意義的物理量都用一個線性厄米算符來表示,可以證明,屬於同一厄米算符的不同本徵函式彼此正交。這種性質稱為本徵函式的正交性。
在量子力學裡,表達粒子的量子態的波函式必須滿足歸一條件,也就是說,在空間內找到粒子的機率必須等於1。這性質稱為歸一性。
基本原理
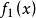 正交歸一化函式
正交歸一化函式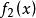 正交歸一化函式
正交歸一化函式若兩個函式和滿足關係式:
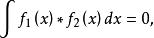 正交歸一化函式
正交歸一化函式則稱這兩個函式正交。量子力學表明:屬於同一厄米算符的不同本徵值的本徵函式互相正交。這種性質稱為本徵函式的正交性。
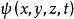 正交歸一化函式
正交歸一化函式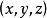 正交歸一化函式
正交歸一化函式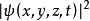 正交歸一化函式
正交歸一化函式描述體系狀態的波函式只有相對的意義,例如,體系處於處的幾率密度只是與成正比,波函式整體乘以一個常數,仍描述同一狀態。為了計算方便,人們約定標準的波函式應滿足下列條件:
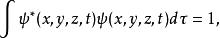 正交歸一化函式
正交歸一化函式這稱為歸一化條件,選擇適當的常數使波函式滿足上式的過程稱為歸一化。
 正交歸一化函式
正交歸一化函式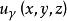 正交歸一化函式
正交歸一化函式有些算符的本徵值取連續譜,這些算符的本徵函式不能滿足上式,應選擇適當的常數使它們滿足:
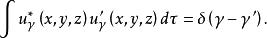 正交歸一化函式
正交歸一化函式 正交歸一化函式
正交歸一化函式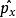 正交歸一化函式
正交歸一化函式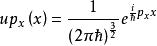 正交歸一化函式
正交歸一化函式 正交歸一化函式
正交歸一化函式這個過程稱為把本徵函式歸一化為函式。例如動量算符的本徵函式就是歸一化為函式的。

