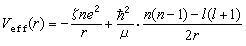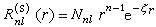斯萊特函式
正文
在原子和分子的自洽場計算 (SCF)中常採用的一種基函式,英文縮寫STO。它是在類氫離子的原子軌道的基礎上提出來的,類氫離子原子軌道的徑向部分Rnl(r)是電子與核的距離r的多項式函式,形式複雜,用於分子積分的計算極為困難,為克服這一困難,J.C.斯萊特提出一種簡化的解析形式: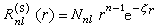
儘管斯萊特函式是自洽場原子軌道一個好的近似,但R埰(r)與類氫軌道中的Rnl(r)有所不同:①R埰(r)無徑向節面,因而單一斯萊特函式所描述的徑向分布圖像將偏離類氫軌道提供的電子徑向分布幾率圖像。② R埰(r)不相互正交,即對類氫軌道有以下關係式:
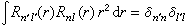
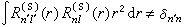
 當然也可採用施密特方法將其正交化。③類氫軌道是電子具有位能 V(r)=-Ze2/r時單電子薛丁格方程的解,式中Z為原子序數。而STO是電子具有有效位能:
當然也可採用施密特方法將其正交化。③類氫軌道是電子具有位能 V(r)=-Ze2/r時單電子薛丁格方程的解,式中Z為原子序數。而STO是電子具有有效位能: