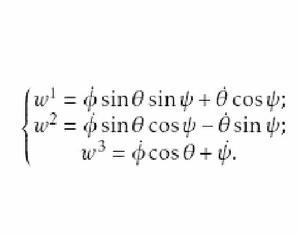基本介紹
 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程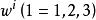 歐拉運動學方程
歐拉運動學方程假定剛體固結參考系 在慣性參考系 中有旋轉運動, 瞬時旋轉角速度為 ,三個分量記為 。
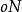 歐拉運動學方程
歐拉運動學方程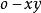 歐拉運動學方程
歐拉運動學方程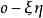 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程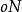 歐拉運動學方程
歐拉運動學方程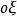 歐拉運動學方程
歐拉運動學方程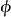 歐拉運動學方程
歐拉運動學方程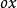 歐拉運動學方程
歐拉運動學方程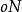 歐拉運動學方程
歐拉運動學方程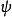 歐拉運動學方程
歐拉運動學方程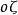 歐拉運動學方程
歐拉運動學方程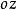 歐拉運動學方程
歐拉運動學方程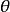 歐拉運動學方程
歐拉運動學方程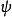 歐拉運動學方程
歐拉運動學方程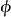 歐拉運動學方程
歐拉運動學方程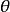 歐拉運動學方程
歐拉運動學方程本體赤道面 與平均赤道面 有一個交線,從原點 沿上述交線的一方引伸出一個射線,稱之為 節線 ,節線與 之間的夾角稱為 進動角,用 表示;瞬時軸 與 之間的夾角稱為 自轉角,用 表示; 與 之間的夾角稱為 章動角,用 表示。自轉角 、進動角 和章動角 通稱Euler角,是由Euler引進的。三個Euler角可以完全描述任意一個剛體的旋轉運動,原因在於:一個點由三個獨立坐標描述;一個剛體通常需要不在同一條直線上的三個點(共9個坐標)來描述;將其中的一個點選為原點,則只需要2個點即6個坐標來描述;但3個點之間存在3個距離方程,因而獨立的坐標數只有3個;3個Euler角正好構成一組獨立坐標。在事先不知道剛體的旋轉運動規律的前提下,要想確定這種旋轉運動,則需要求解Euler運動學方程和Euler動力學方程。
方程形式
根據三個Euler角的定義不難寫出如下關係:
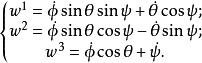 歐拉運動學方程
歐拉運動學方程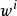 歐拉運動學方程
歐拉運動學方程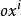 歐拉運動學方程
歐拉運動學方程其中 表示繞地固質心坐標系 軸的旋轉角速度。上式便是著名的 Euler運動學方程,即 歐拉 運動學方程。
準慣性系中的表達形式
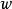 歐拉運動學方程
歐拉運動學方程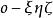 歐拉運動學方程
歐拉運動學方程將旋轉角速度 在準慣性系 中表示出來:
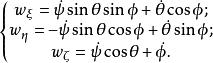 歐拉運動學方程
歐拉運動學方程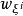 歐拉運動學方程
歐拉運動學方程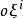 歐拉運動學方程
歐拉運動學方程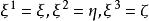 歐拉運動學方程
歐拉運動學方程其中 表示繞地心準慣性坐標系 軸的旋轉角速度( )。
相關概念
歐拉角
 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程剛體定點運動的自由度為3,如何選擇3個變數,使它們既能簡單、明確、單值地確定剛體位置,又能獨立變化,這對簡化定點運動的描述是非常重要的,剛體力學的奠基者歐拉(Leonhard Euler,1707一1783)成功地、巧妙地解決了這個問題,他選擇3個角度,即著名的歐拉角(Euler angles)作為描述剛體定點運動的變數,具體選擇方法如下:以固定點為原點建立靜正坐標系 ,再以固定點為原點建立與剛體固連的動坐標系 如圖1。
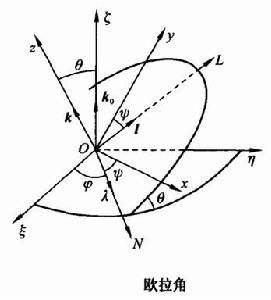 圖1
圖1 歐拉運動學方程
歐拉運動學方程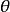 歐拉運動學方程
歐拉運動學方程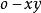 歐拉運動學方程
歐拉運動學方程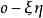 歐拉運動學方程
歐拉運動學方程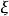 歐拉運動學方程
歐拉運動學方程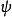 歐拉運動學方程
歐拉運動學方程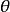 歐拉運動學方程
歐拉運動學方程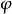 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程確定剛體位置等價於確定動坐標的位置,他用兩個角度確定z軸的位置,一個是z軸對 軸的傾角 角,另一個是用來確定z軸的方位,它是 面與平均赤道面 面的交線ON與 軸的夾角,交線ON稱為 節線;這兩個角確定後,z軸的位置就確定了,但動坐標系還可以繞z軸轉動,若動坐標的x軸與節線的夾角 確定了,則動坐標的位置完全確定,這樣選取的3個角 , , 稱為 歐拉角。
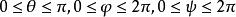 歐拉運動學方程
歐拉運動學方程它們的量度方向如圖所示,它們的變化範圍分別為: 。
這3個角可以獨立變化,即這3個變數是獨立的,從運動學上,它們之間不存在依賴關係(即函式關係),最能說明其獨立性的事實是:當任何一個角自由改變時,其他兩個角可以保持不變,如以下三種情況是可能的。
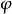 歐拉運動學方程
歐拉運動學方程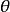 歐拉運動學方程
歐拉運動學方程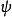 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程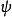 歐拉運動學方程
歐拉運動學方程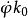 歐拉運動學方程
歐拉運動學方程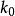 歐拉運動學方程
歐拉運動學方程 歐拉運動學方程
歐拉運動學方程1. 僅 角改變,保持 , 不變。這種運動相應於z軸與 軸間夾角不變,z軸在靜止空間中沿圓錐面運動,同時 角也保持不變,這種運動稱為 進動(precession),相應的角速度稱為 進動角速度,它的大小和方向為 , 為 軸的單位矢量。
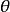 歐拉運動學方程
歐拉運動學方程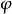 歐拉運動學方程
歐拉運動學方程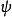 歐拉運動學方程
歐拉運動學方程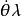 歐拉運動學方程
歐拉運動學方程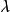 歐拉運動學方程
歐拉運動學方程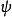 歐拉運動學方程
歐拉運動學方程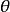 歐拉運動學方程
歐拉運動學方程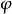 歐拉運動學方程
歐拉運動學方程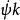 歐拉運動學方程
歐拉運動學方程2. 僅角改變,保持,角不變。剛體的這種運動稱為章動(nutation),相應的角速度為章動角速度,它的大小和方向為,為沿節線的單位矢量。
3. 僅角改變,保持,角不變。剛體的這種運動稱為自轉(rotation),相應的角速度為,稱為自轉角速度,k為z軸的單位矢量。
當3個角同時變化,三種運動同時存在時,剛體的角速度為3個分角速度的合成。
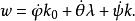 歐拉運動學方程
歐拉運動學方程