剛體定點轉動的動量矩
剛體繞固定點O轉動時對點O的動量矩是描述剛體轉動運動的主要動力學量。動量矩的表達式是 L= Jω，式中 J為剛體對O點的慣量張量（見轉動慣量）， ω為剛體轉動的角速度矢量。過點O作直角坐標系Oxyz，則動量矩在坐標系Oxyz中的矩陣表達式為：
剛體定點轉動動力學當坐標系Oxyz為剛體對點O的主軸坐標系時，慣性積為零，動量矩的表達式為：
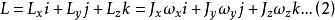剛體定點轉動動力學一般情況下，動量矩矢量、角速度矢量及慣量主軸不共線。
歐拉動力學方程
剛體定點轉動動力學將對固定點O的動量矩定理，向固結與剛體的主軸坐標系投影，即為剛體 定點轉動的動力學方程：
剛體定點轉動動力學上式是歐拉建立的剛體繞定點的運動與所受外力矩之間的關係，稱為歐拉動力學方程。如果以歐拉角ψ，θ，φ描述剛體的方位，則還有歐拉運動學方程：
剛體定點轉動動力學
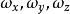剛體定點轉動動力學方程（3）與（4）共同組成封閉的方程組，6個變數ψ，θ，φ，，總階數是6階，反映了定點轉動運動的自由度數是3。還需指出，用分析力學中的拉氏第二方程也能建立剛體定點轉動的動力學方程，但是方程冗長而複雜，只有在對稱剛體的特殊情況下才方便處理。
動力學方程的積分
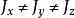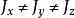剛體定點轉動動力學 剛體定點轉動動力學
剛體定點轉動動力學
剛體定點轉動動力學
剛體定點轉動動力學經過百餘年的研究，證實只在三種情況下方程組（3）、（4）可給出解析解，即：1、歐拉情況（1765），指剛體的質量分布可以任意，，而外力矩為零，即定點位於剛體的重心。這時剛體作自由運動，其運動圖像相當於一個橢球在固定平面上作滑動的滾動。2、拉格朗日情況（1788），指剛體是對稱的，而重心在對稱軸上，，其運動圖像是進動與章動的疊加。3、柯瓦列夫斯卡婭情況（1888），指一種特殊的對稱剛體，即，而重心在赤道平面上，，這時剛體的運動具有非周期性。對於這三種古典情況，可求得動力學方程對任意初始條件的通解，但有實際意義的往往不屬於這三種情況。此後人們尋求滿足某一特定初始條件的特解，並研究此特解代表的特定運動的穩定性。如果運動是穩定的，如無外力矩的剛體繞過定點某軸作永久轉動，即轉軸在空間的方位不變，轉動角速度不變的情況，實際上是可以實現的。陀螺儀器出現以後，由於陀螺高速自轉，因而有可能對定點轉動的動力學方程求近似解，出現了高速自轉下的陀螺近似理論。（見陀螺力學）
