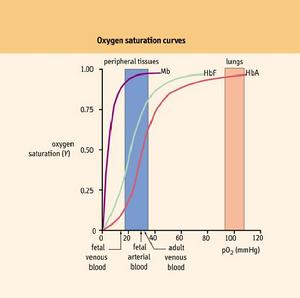
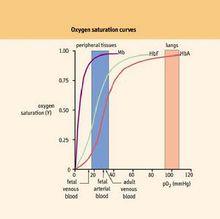
 滿載飽和曲線
滿載飽和曲線氧的飽和曲線
微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。曲線的更嚴格的定義是區間【α,b)】到E3中的映射r:【α,b)】→E3。有時也把這映射的像稱為曲線。具體地說,設Oxyz是歐氏空間E3中的笛卡兒直角坐標系,r為曲線C上點的向徑,飽和:在一定溫度和壓力下,溶液所含溶質的量達到最大限度,不能再溶解。曲線論的基本公式 設正則曲線C的參數方程為r=r(s),s是弧長參數,p(s)是曲線C上參數為s即向徑為r(s)的一個定點。Q(s+Δs)為C上鄰近p的點,Q沿曲線C趨近於p時,割線pQ的極限位置稱為曲線C在p點的切線。過p點與切線垂直的平面稱為曲線C在p點的法平面。曲線C在p點的切線及C上鄰近點R確定一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面。p點的法線稱為曲線C在p點的主法線(圖2)。
以"·"表示關於弧長參數s的導數,並且設那么和b(s)=t(s)×n(s)分別是曲線C在p(s)點的切線、主法線和次法線上的單位向量,並且t(s)指向曲線C的正向。n(s)指向曲線凹入的一方。t(s)、n(s)和b(s)按此順序構成右手系,且分別稱為曲線C在p(s)點的切向量、主法向量和次法向量。{r(s),t(s),n(s),b(s)}稱為曲線C在p(s)點的弗雷內標架。曲線C的每一點都有弗雷內標架。為研究曲線上兩個鄰近點上弗雷內標架之間的變換關係,要討論t(s)、n(s)和b(s)關於s的導向量,它們可由標架向量線性表出,這就是下述曲線論的基本公式(弗雷內公式):
式中k(s)和τ(s)分別被稱為曲線C在p(s)點的曲率和撓率。
曲率 這裡是切向量t(s)和t(s+Δs)之間的夾角。故曲率度量了曲線上相鄰兩點的切向量的夾角關於弧長的變化率。直線的曲率恆為0。圓周的曲率等於其半徑的倒數。當曲線C在p(s)點的曲率k≠0時,在p(s)點的主法線上沿n(s)的正向取點Q,使得pQ=1/k,在p點的密切平面上以Q為中心,1/k為半徑的圓稱為曲線C在p點的曲率圓或密切圓,Q和1/k分別稱為曲率中心和曲率半徑。密切圓是過曲線C上p(s)點和鄰近兩點的圓的極限位置。
撓率撓率,它的絕對值度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。
若p0(s0)點的曲率和撓率均不為零,取p0為原點,曲線的切線、主法線和次法線為坐標軸,在p0附近,曲線可近似地表示為:所以曲線C在p0點鄰近的近似形狀如圖3所示。
曲線論的基本定理 曲線的弧長s、曲率k(s)和撓率τ(s)是運動的不變數。反過來,曲線的曲率和撓率也完全決定了曲線的形態。具體地說,如果給定了兩個連續函式k(s)>0和τ(s),s∈【α,b)】,則存在以k(s)和τ(s)分別為其曲率和撓率的曲線,並且這些曲線經過空間的一個運動可以互相疊合。