欠角

欠角

具體定義如下：凸多面體與一個頂點相關的面角之和與360度的差稱為該頂點的欠角。 性質凸多面體各頂點的欠角之和為720度。 四面體一共有四個頂點，而且完全相同，因此四個頂點的欠角和為720度。

定義

欠角是為了研究凸多面體而形成的定義，該定義的引出是為了更好地認識三維空間中的凸多面體，能夠更快認識到圖多面體的性質。
具體定義如下：凸多面體與一個頂點相關的面角之和與360度的差稱為該頂點的欠角。

性質

凸多面體各頂點的欠角之和為720度。該性質可以由歐拉定理證明。
詳細證明如下：
設V，S，E分別是凸多面體的頂點集，面集和邊集。由歐拉定理可得\left|V\right|+\left|S\right|-\left|E\right|=2，設a_{ij}為與頂點v_i，面s_j形成的相關面角，e_j為s_j的邊數，給定s_j則\sum_{v_j\in V}a_{ij}=\left(e_j-2\right)
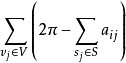
\sum_{v_j\in V}\left(2\pi-\sum_{s_j\in S}a_{ij}\right)
=\sum_{v_j\in V}2\pi-\sum_{v_j\in V}\sum_{s_j\in S}a_{ij}
=2\left|V\right|\pi-\sum_{v_j\in V}\sum_{s_j\in S}a_{ij}
=2\left|V\right|\pi-\sum_{s_j\in S}\left(e_j-2\right)\pi
=2\left|V\right|\pi-\sum_{s_j\in S}e_j\pi+2\left|S\right|\pi
=2\left|V\right|\pi+2\left|S\right|\pi-2\left|E\right|\pi
=4\pi

套用

欠角以及欠角和的套用舉例如下：
以正四面體為例，正四面體的每個面都是正三角形，因此每個面的內角為60度。
每個頂點上都有三個面角，則該頂點三個面角之和為180度。
則根據定義可得，每個頂點的欠角為360-180=180度。
四面體一共有四個頂點，而且完全相同，因此四個頂點的欠角和為720度。
該定理可以幫助認識新的凸多面體，如足球等凸多面體，幫助分析組合數學的Polya定理中涉及的凸多面體轉動群。

相關詞條

相關搜尋

熱門詞條

聯絡我們