定律定義
凸多面體與一個頂點相關的面角之和與360度的差稱為該頂點的欠角 。
凸多面體各頂點欠角的和為720度 (可以使用歐拉定理 證明)。
推導過程
 欠角和定理
欠角和定理 欠角和定理
欠角和定理 欠角和定理
欠角和定理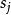 欠角和定理
欠角和定理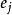 欠角和定理
欠角和定理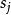 欠角和定理
欠角和定理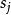 欠角和定理
欠角和定理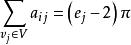 欠角和定理
欠角和定理設V,S,E分別是凸多面體的頂點集,面集和邊集。由歐拉定理 可得 ,設 為與頂點 ,面 形成的相關面角, 為 的邊數,給定 則 。
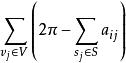 欠角和定理
欠角和定理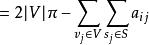 欠角和定理
欠角和定理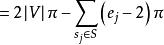 欠角和定理
欠角和定理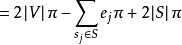 欠角和定理
欠角和定理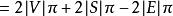 欠角和定理
欠角和定理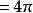 欠角和定理
欠角和定理實驗驗證
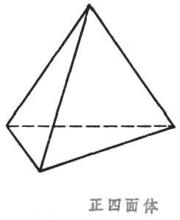 正四面體
正四面體以正四面體為例,欠角和定理驗證如下:
對於正四面體,正四面體的每個面都是正三角形,因此每個面的內角為60度。
每個頂點上都有三個面角,則該頂點三個面角之和為180度。
則根據定義可得,每個頂點的欠角為360-180=180度。
四面體一共有四個頂點,而且完全相同,因此四個頂點的欠角和為720度。
適用範圍
該定理可以幫助認識新的凸多面體,如正十二面體、正二十面體、足球等凸多面體,並結合歐拉定理 對這些多面體的頂點數、邊數和面數進行數量上的分析,而且該定理對幫助分析組合數學的Polya定理 中涉及的凸多面體轉動群很有作用。
套用領域
·認識和分析正十二面體
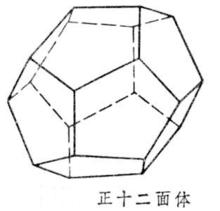 正十二面體
正十二面體例如在分析用正五邊形搭成的最多的正多面體可以搭建成正多少面體時,可以做如下分析:
正五邊形的內角=(5-2)·180°/5=108°
因為正十二面體的一個頂點連線三個面,
所以正十二面體的欠角=360°-3·108° =36°。
則根據欠角和定理,共有:720°/36°=20(個頂點)
一個頂點連線3條棱,重複度為2:20·3/2=30條棱
一個頂點相關3個面,重複度為5:20·3/5=12個面
·認識和分析正二十面體
例如在分析用正3角形搭成的面最多的正多面體可以搭建成正多少面體時,可以做如下分析:
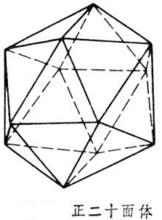 正二十面體
正二十面體正六邊形的內角=(3-2).180°/3=60°,
因為正二十面體的一個頂點連線五個面,
所以正二十面體的欠角=360°-5·60° =60° 。
則根據欠角和定理,共有:720°/60°=12(個頂點)
一個頂點關聯5條棱,重複度為2:12·5/2=30條棱
一個頂點關聯5個面,重複度為3:12·5/3=20個面
·認識和分析足球
例如可以分析足球的頂點個數、棱個數、面個數、以及足球中的正五邊形和正六邊形的個數:
 足球
足球對於足球而言,正五邊形內角108°,正六邊形內角120°。
因為足球的一個頂點連線一個正五邊形和兩個正六邊形,
所以正二十面體的欠角=360°–(108°+2·120° )=12°,
則根據欠角和定理,共有:720°/12 =60(個頂點),
一個頂點關聯3條棱,重複度為2:60·3/2=90(條棱)。
一個頂點關聯一個正五邊形,重複度為5:60/5=12(個5邊形)
一個頂點關聯兩個正六邊形,重複度為6:60·2/6=20(個6邊形)
