定義
對於隨機變數X的分布函式F（x），如果存在非負可積函式f(x)，使得對任意實數x,有
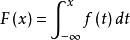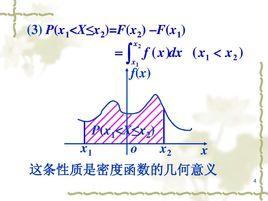
機率密度則X為連續型隨機變數，稱f(x)為X的機率密度函式，簡稱為機率密度。
單純的講機率密度沒有實際的意義，它必須有確定的有界區間為前提。可以把機率密度看成是縱坐標，區間看成是橫坐標，機率密度對區間的積分就是面積，而這個面積就是事件在這個區間發生的機率，所有面積的和為1。所以單獨分析一個點的機率密度是沒有任何意義的，它必須要有區間作為參考和對比。
性質
非負性
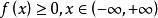機率密度規範性
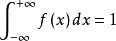機率密度這兩條基本性質可以用來判斷一個函式是否為某一連續型隨機變數的機率密度函式。
機率密度
定理：設隨機變數X具有機率密度f(x)，-∞<x<∞，由設函式g(x)處處可導且恆有g'(x)>0（或恆有g'(x)<0），則Y=g(X)是連續型隨機變數，其機率密度為
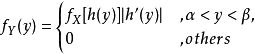機率密度其中α=min(g(-∞),g(∞))，β=max(g(-∞),g(∞))，h(y)是g(x)的反函式。
物理概念
氫原子3P軌道千萬次合成機率密度波函式圖象電子運動的狀態有波函式Ψ來描述，|Ψ|²表示電子在核外空間某處單位體積內出現的機率，即機率密度。處於不同運動狀態的電子，它們的|Ψ|各不相同，|Ψ|²當然也不同。密度大則事件發生的分布情況多，反之亦然。若用黑點的疏密程度來表示各個電子機率密度的大小，則|Ψ|²大的地方黑點較密，其機率密度大，反之亦然。在原子和外分布的小黑點，好像一團帶負電的雲，把原子核包圍起來，人們稱它為電子云。
1926年，奧地利物理學家薛丁格運用偏微分方程，建立了描述微觀粒子運動的波動方程，即 薛丁格方程。由薛丁格方程式的可知，對於一個質量為m，在勢能為 V的勢場中運動的微粒來說，有一個與這個微粒運動相聯繫的波函式ψ，這個波函式就是薛丁格方程的一個合理的解，每一個解都與相應的常數E對應，就是微粒在這一運動狀態的能量（或能級）。|Ψ|²表示原子核外空間某點P(x,y,z)處電子出現的 機率密度，即在該點處單位體積中電子出現的機率。用來表示機率密度的幾何圖形俗稱電子云，電子云並非眾多電子彌散在核外空間，而是電子在核外空間各處出現的機率密度的形象表現。
氫原子的機率分布圖