樣本
樣本(specimen)是觀測或調查的一部分個體,總體是研究對象的全部。
總體中抽取的所要考查的元素總稱,樣本中個體的多少叫樣本容量。
如作水質檢驗時從井水或河水中采的水樣,臨床化驗中從病人身上采的血液或其它活體組織標本,是樣本;而整個一口井或一條河的某一段所有的水,某病人全身所有的血液或某個組織器官,則是總體。這類總體是具體存在的,但另有些總體卻是假想的,只是理論上存在的一個範圍。例如試驗某一治療流感新藥的療效,最初接受治療的一批流感患者,不論數量多少,都只是一個樣本。若該藥療效得到肯定,從而加以推廣,那么此後凡在相同條件下接受該藥治療的所有流感患者,都屬於這個總體。可是當初試用時,這個總體還並不存在,是假想的。
總體包含的觀察單位通常是大量的甚至是無限的,在實際工作中,一般不可能或不必要對每個觀察單位逐一進行研究。我們只能從中抽取一部分觀察單位加以實際觀察或調查研究,根據對這一部分觀察單位的觀察研究結果,再去推論和估計總體情況。如上述某新藥治療流感例子,試驗治療的只是少數有限的病人,而結論卻要推廣到全體,得出一個該藥對所有流感患者之療效的規律性的認識。所以說,觀察樣本的目的在於推論總體,這就是樣本與總體的辯證關係。
標準差
標準差(Standard Deviation),在機率統計中最常使用作為統計分布程度(statistical dispersion)上的測量。標準差定義是總體各單位標準值與其平均數離差平方的算術平均數的平方根。它反映組內個體間的離散程度。測量到分布程度的結果,原則上具有兩種性質:為非負數值, 與測量資料具有相同單位。一個總量的標準差或一個隨機變數的標準差,及一個子集合樣品數的標準差之間,有所差別。
標準差表示的就是樣本數據的離散程度。標準差就是樣本平均數方差的開平方,標準差通常是相對於樣本數據的平均值而定的,通常用M±SD來表示,表示樣本某個數據觀察值相距平均值有多遠。從這裡可以看到,標準差受到極值的影響。標準差越小,表明數據越聚集;標準差越大,表明數據越離散。標準差的大小因測驗而定,如果一個測驗是學術測驗,標準差大,表示學生分數的離散程度大,更能夠測量出學生的學業水平;如果一個測驗測量的是某種心理品質,標準差小,表明所編寫的題目是同質的,這時候的標準差小的更好。標準差與常態分配有密切聯繫:在常態分配中,1個標準差等於常態分配下曲線的68.26%的面積,1.96個標準差等於95%的面積。這在測驗分數等值上有重要作用。
分析法
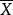 樣本標準差
樣本標準差定義 為樣本均值,S一樣本標準差。
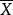 樣本標準差
樣本標準差樣本是受審查客體的反映形象或其自身的一部分。樣本取得越多越能接近實際情況。樣本均值是所有的樣本求樣平均值,反映數組中波動所圍繞的中心,計算公式為:
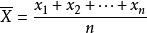 樣本標準差
樣本標準差樣本偏離樣本均值的標準差來衡量數組的離散程度。樣本標準差的計算公式為:
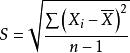 樣本標準差
樣本標準差合併
對一個完整的測量過程,其測量結果的不確定度是通過對各個分項不確定度分別評定而導出的;其中測量重複性是測量過程中必然存在的不確定的分量之一。但在實際工作中,各類計量檢定活動中所開展的檢定、校準、檢驗等規範測量工作,其涉及被檢(測)件的數量極多,因此不可能採用貝塞爾法來評定每一被檢(測)件由於測量重複性引人測量結果的不確定度。
為解決計量檢定工作中大量儀表的測量不確定度評定需要,可直接採用預先評定的結果來評估測量重複性可能引人的不確定度。其方法是取若干樣本,每個樣本均用貝塞爾法計算出樣本的實驗標準差,然後將各個實驗標準差進行合併(或平均),即為合併樣本標準差,最後以合併樣本標準差來計算被檢(測)儀器引人的不確定度分量。
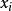 樣本標準差
樣本標準差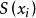 樣本標準差
樣本標準差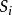 樣本標準差
樣本標準差合併樣本標準差的基本思想是:對處於統計控制狀態下的測量過程,被測量X的單次測量結果 的標準差 可以認為相等。這一思想可以進一步推廣到性質相同的不同觀測結果。譬如,根據計量檢定規程,在某一儀器全量程範圍內均勻選取m個檢定點,每個點重複測量n(n通常較小,如為2等)次;當對各點n次測量值所計算的實驗標準差 沒有明顯差異時,則可用合併樣本標準差的思想方法,評定計算各受檢點由測量重複性而引起的不確定度分量,其計算公式如公式下。
每個測量點單次測量結果的標準不確定度計算公式為:
 樣本標準差
樣本標準差而每個測量點n次測量平均值的測量結果標準不確定度計算公式為:
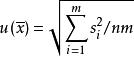 樣本標準差
樣本標準差套用
帶鋼板面劃傷
酒鋼的鍍鋅機組設計年產量為75萬t,該機組生產連續性強、對表面質量要求高,其產品以生產家電板、鍍鋁鋅板為主,已遠銷國內外市場。自2010年投產以來在解決帶鋼劃傷缺陷方面經歷了漫長的過程。劃傷缺陷的來源主要有原料基板、機械刮擦、速度不匹配等。隨著技術經驗的積累,能逐步識別出原料基板帶來的缺陷,而對鍍鋅線自身輥面產生的劃傷卻缺少判斷方法。輥面劃傷主要是由於帶鋼與輥面間的相互滑動產生,主要原因有輥徑不符、輥面凸起、轉速偏差。如何判斷是速度偏差造成的劃傷、偏差值達到多少能造成劃傷,需要建立一種新的分析識別方法。陳代兵等經過探討研究,將樣本標準差理論運用到分析中,推出了一套針對該缺陷的分析方法,能將缺陷來源定性並及時消除。
精密壓力表示值誤差不確定度評定
精密壓力表具有結構簡單、性價比高的特點,長期以來廣泛套用於工農業生產和科研試驗,甚至被用作檢定一般壓力表的標準設備。但在常規的計量檢定、校準和測試工作中,計量人員通常忽略對其示值誤差的不確定度進行評定,以致儀表用戶或檢測人員無法判斷其測量數據的準確度。究其原因,主要是由於在精密壓力表示值誤差不確定度分析過程中,對由於測量重複性引人的不確定度分量的分析計算極其繁雜,需要的工作量過大而造成的。
趙本義等通過對常用的精密壓力表示值誤差不確定度評定方法進行分析,提出採用合併樣本標準差評定測量重複性引人不確定度項的方法,並對兩種分析方法進行比較論述,以簡化精密壓力表示值誤差不確定度評定過程,從而實現快速分析精密壓力表示值誤差不確定度的目標。