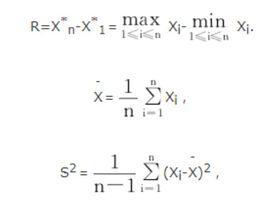基本介紹
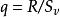 學生化極差
學生化極差 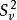 學生化極差
學生化極差 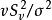 學生化極差
學生化極差 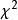 學生化極差
學生化極差 學生化極差亦稱“t化極差”,是極差R與樣本標準差之比。主要用於正態總體 N(μ,σ ),兩種基本形式:1) d=R/ S,其中S是修正樣本標準差;2),其中是σ 的無偏估計, 與R獨立且服從自由度為ν 的分布。t化極差主要用於多重比較和建立R的置信(預測)區間, 統計量d和q都有編制好的臨界值表 。
相關分析
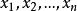 學生化極差
學生化極差 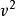 學生化極差
學生化極差 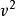 學生化極差
學生化極差 設是容量為n的隨機樣本,來自平均數為0和方差為1的正態密度,再設是自由度為m的卡方分布,諸x和是獨立的。隨機變數
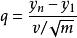 學生化極差
學生化極差 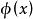 學生化極差
學生化極差 稱為學生化極差(y是x的順序統計量),在某些套用問題中它是重要的 。設N(x)是平均數為0方差為1的正態密度的累積分布,是同一分布的密度函式,那么x的極差分布是
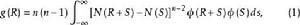 學生化極差
學生化極差 其中
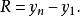 學生化極差
學生化極差 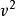 學生化極差
學生化極差 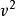 學生化極差
學生化極差 R和的聯合分布,其中是自由度為m的卡方分布,是
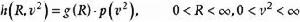 學生化極差
學生化極差 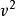 學生化極差
學生化極差 作從R,到q,u的變數變換
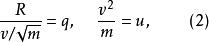 學生化極差
學生化極差 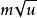 學生化極差
學生化極差 雅可比行列式是,我們得到q和u的聯合密度
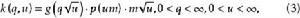 學生化極差
學生化極差 q的密度通過k(q,u)對u積分得到
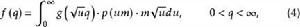 學生化極差
學生化極差 對於n大於2的值,這個函式是很複雜的,但是對a=0.01,0.05和0.10,積分
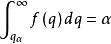 學生化極差
學生化極差 已被製成表。前面所談的可歸納成下述定理 。
定理
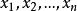 學生化極差
學生化極差 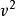 學生化極差
學生化極差 設
是來自平均數為0和方差為1的正態密度的一個隨機樣本,再設是與之獨立的自由度為m的卡方變數,那么
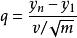 學生化極差
學生化極差 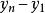 學生化極差
學生化極差 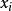 學生化極差
學生化極差 服從自由度為n和m的學生化極差分布,其中是的極差,密度用(4)給出 。