簡介
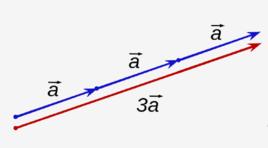
在數學中,標量乘法是由線性代數中的向量空間定義的基本運算(更一般地說,它是抽象代數中的一個模組)。在通常的幾何概念中,通過正實數的歐幾里德向量的標量乘法將矢量的幅值相乘而不改變它的方向。 術語“標量”本身來自於這種用法:標量是向量的幅值。 標量乘法是向量乘以標量(乘積是向量),並且必須與兩個向量的內積(乘積是標量)進行區分。
定義
通常,如果K代表域,V代表K上的向量空間,則標量乘法是從K×V到V的函式。將該函式套用於K中的c、V中的v表示的結果為cv。
屬性
標量乘法符合以下法則:
(1)標量中的加法性:(c + d)v = cv + dv(其中v為向量);
(2)向量中的加法性:c(v + w)= cv + cw(其中v,w為向量);
(3)標量乘積與標量乘法的兼容性:(cd)v = c(dv)(其中v為向量);
(4)乘以1不改變向量:1v = v(其中v為向量);
(5)乘以0給出零向量:0v = 0(其中v為向量);
(6)乘以-1給出加法逆:(-1)v = -v(其中v為向量)。
這裡+是在域或向量空間中的加法;並且0是兩者之間的加性特徵。 並置表示欄位中的標量乘法或乘法運算。
解讀
標量乘法可以被視為外部二進制運算或作為向量空間上的域的運算。 標量乘法的幾何解釋是它通過常數因子來拉伸或收縮向量。
作為特殊情況,可以將V取為K本身,然後可以將標量乘法簡單地作為域中的乘法。
當V為K 時,標量乘法等效於每個分量與標量的乘法,並且可以這樣定義。
如果K是交換環,V是K上的模組,但是沒有加法逆。 如果K不可交換,則可以定義不同的運算左標量乘法cv和右標量乘法vc(其中v為向量)。
矩陣的標量乘法
矩陣A與標量λ的左標量乘法得到與A相同大小的另一矩陣λA。
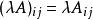 標量乘法
標量乘法更明確的:
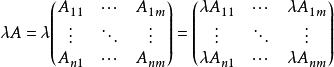 標量乘法
標量乘法類似地,將矩陣A與標量λ的右標量乘法定義為
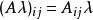 標量乘法
標量乘法更明確的:
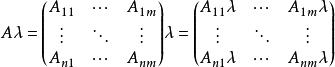 標量乘法
標量乘法當底層環可交換時,例如實數或複數欄位,這兩個乘法相同,簡稱為標量乘法。 然而,對於不可交換的更一般環上的矩陣,例如四元數,它們可能不相等。
對於一個真正的標量和矩陣:
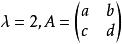 標量乘法
標量乘法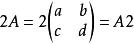 標量乘法
標量乘法對於四元數標量和矩陣:
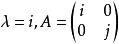 標量乘法
標量乘法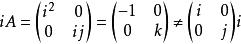 標量乘法
標量乘法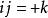 標量乘法
標量乘法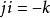 標量乘法
標量乘法其中i,j,k是四元數單位。 四元數乘法的非交換性阻止了改變 到 的轉換。