定義
標準誤差定義為各測量值誤差的平方和的平均值的平方根,故又稱為均方根誤差。
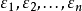 標準誤
標準誤設n個測量值的誤差為
,則這組測量值的標準差σ等於:
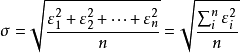 標準誤
標準誤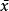 標準誤
標準誤由於被測量的真值是未知數,各測量值的誤差也都不知道,因此不能按上式求得標準誤差。測量時能夠得到的是算術平均值(
),它最接近真值(
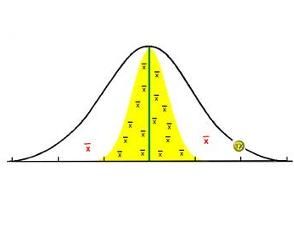
),而且也容易算出測量值和算術平均值之差,稱為殘差(記為v)。可以用殘差v表示有限次(n次)觀測樣本的標準差s,其計算公式為:
 標準誤
標準誤對於一組等精度測量(n次測量)數據的算術平均值,其誤差應該更小些。則標準誤等於:
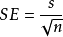 標準誤
標準誤標準誤與標準差
標準差與標準誤都是數理統計學的內容,兩者不但在字面上比較相近,而且兩者都是表示距離某一個標準值或中間值的離散程度,即都表示變異程度,但是兩者是有著較大的區別的。
首先要從統計抽樣的方面說起。現實生活或者調查研究中,我們常常無法對某類欲進行調查的目標群體的所有成員都加以施測,而只能夠在所有成員(即樣本)中抽取一些成員出來進行調查,然後利用統計原理和方法對所得數據進行分析,分析出來的數據結果就是樣本的結果,然後用樣本結果推斷總體的情況。一個總體可以抽取出多個樣本,所抽取的樣本越多,其樣本均值就越接近總體數據的平均值。
表示的就是樣本數據的離散程度。標準差就是樣本平均數方差的開平方,標準差通常是相對於樣本數據的平均值而定的,通常用M±SD來表示,表示樣本某個數據觀察值相距平均值有多遠。從這裡可以看到,標準差受到極值的影響。標準差越小,表明數據越聚集;標準差越大,表明數據越離散。標準差的大小因測驗而定,如果一個測驗是學術測驗,標準差大,表示學生分數的離散程度大,更能夠測量出學生的學業水平;如果一個測驗測量的是某種心理品質,標準差小,表明所編寫的題目是同質的,這時候的標準差小的更好。標準差與常態分配有密切聯繫:在常態分配中,1個標準差等於常態分配下曲線的68.26%的面積,1.96個標準差等於95%的面積。這在測驗分數等值上有重要作用。
標準誤
表示的是抽樣的誤差。因為從一個總體中可以抽取出無數多種樣本,每一個樣本的數據都是對總體的數據的估計。標準誤代表的就是當前的樣本對總體數據的估計,標準誤代表的就是樣本均數與總體均數的相對誤差。標準誤是由樣本的標準差除以樣本容量的開平方來計算的。從這裡可以看到,標準誤更大的是受到樣本容量的影響。樣本容量越大,標準誤越小,那么抽樣誤差就越小,就表明所抽取的樣本能夠較好地代表總體。
