內容簡介
核密度Vautherin和Brink 將Skyrme型 力套用於核體系，利用這種數學處理上比較簡單的等效核力形式進行Hartree-Fock（H-F）計算，在研究基態核的性質方面有了很大進展。這種H-F方法陸續套用於重核裂變位壘、超形變態核性質、巨共振求和規則（sum rules）、有溫度的“熱”核等方面，取得了很好的效果。儘管如此，H-F微觀計算面對實際核的套用仍有其局限性，事實上，Skyrme型等效核力的核參量遠沒有精確確定，至少有十幾種較流行的Skyrme勢參量組。它們都是通過擬合幾個球形核的結合能而選定的，沒有對大量基態核質量進行驗算，而且大部分Skyrme勢參量組給出的核裂變位壘計算值都偏高，對遠離β穩定線的核性質計算結果也有歧義。
Thomas-Fermi方法中適用的新式核密度
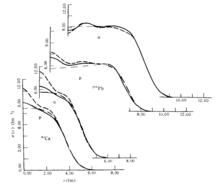用etf, evm , H-F方法分別給出40Ca 和208Pb的中子、質子密度分布套用推廣的Thomas-Fermi方法（ETF）於Skyrme型等核效力，可將基態平均能量表示為中子和質子密度分布的泛函，再對該能量密度泛函做變分極小化，就可以得到平均的H-F能量，加上殼修正就可以再現H-F殼模型計算結果。對能量密度泛函直接做變分極小化，需要求解Euler-Lagrange方程，這個方法對球形核的求解也很不容易，更難推廣到變形核。ETF方法一般先給定極小化密度的函式形式。由於ETF方法計算簡便，其套用範圍容易擴展，不僅對核基態和裂變位壘的計算很成功，而且對高自旋態、相對論推廣、巨共振能量等方面也進行了廣泛計算。T6系列Skyrme勢參量組，利用ETF加微觀修正的方法對大量核基態實驗數據擬合，給出了SkSC勢參量組，其中試探核密度形式利用了純Fermi函式形式。
其實，用純Fermi函式代替ETF函式形式作為試探核密度，由輕核到重核，ETF的極小化能量相差2-5MeV，這個差距可以通過調整Skyrme勢參量的方法來補償。之所以用這種曲折的計算方法，主要是ETF函式形式有10個由極小化決定的參量，對於擬合幾千個核數據計算量仍太大，核密度的計算不精確。
原子核的核密度經驗公式
經驗公式
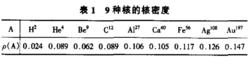9種核的核密度Frankfun和strikman提出的核密度模型認為核子結構函式的核效應是由原子核的核密度不同造成的。但是，對於大多數核，由於缺少實驗數據它們的核密度並不知道。為了對其核效應進行理論研究，又迫切需要知道這些核的核密度。為此，採用唯象的方法，從下述兩個方面出發尋找原子核的核密度經驗公式。
（1）表1給出的9種核的核密度值，是尋找和檢驗參數公式的出發點和重要參考。由表1給出的核密度，是通過原子核電磁半徑平方平均值(r )的實驗數據求出原子核等效均勻半徑R，進而得出ρ(A)的值。但是，由於實驗數據存在著一定的誤差，通過原子核電磁半徑平方平均值(r )的實驗數據求出原子核等效均勻半徑尺和核密度ρ(A)，有一定的不確定範圍，因此，這些核密度又有小量的可調性。基於這樣兩個特點，使得我們能夠擬合已有核的核密度，做出核密度隨A變化的光滑連續曲線。
（2）通過建立核密度與原子核平均結合能之間的聯繫，尋找核密度經驗公式。核密度模型認為核密度隨A的變化描述的是原子核內的核子與自由核子的差異，是核效應的一種描述；在核物理學中，原子核的結合能也是描述原子核內的核子與自由核子的差異，也是核效應的一種描述。它們是從不同側面描述著自由核子組成原子核時產生的核效應。據此推測，它們之間應當有某種聯繫。
經驗公式的有效性檢驗
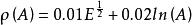核密度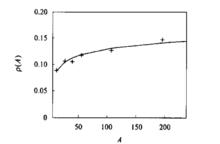
圖1 核密度隨核質量數A的變化曲線採用這些值並利用推廣了的核密度模型計算了核效應函式R（x，Q），並與實驗結果進行了比較。
公式適用範圍，其一，對於A<12的輕核，原子核的液滴模型只給出結合能的平均結果，沒有能顯示出起伏，即沒有給出各核的結合能的確切值；其二，輕核的核效應並不明顯，人們的注意力主要集中於研究A≥12的核的核效應。
