簡介
核密度估計是在機率論中用來估計未知的密度函式,屬於非參數檢驗方法之一,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。假設我們有n個數X1-Xn,我們要計算某一個數X的機率密度有多大。核密度估計的方法是這樣的:
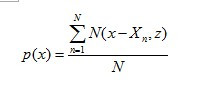
其中N(x,z)為正太分布的機率密度函式,z為設定的參數。
基本原理
在我們對某一事物的機率分布的情況下。如果某一個數在觀察中出現了,我們可以認為這個數的機率密度很比大,和這個數比較 近的數的機率密度也會比較大,而那些離這個數遠的數的機率密度會比較小。基於這種想法,針對觀察中的第一個數,我們都可以f(x-xi)去擬合我們想像中 的那個遠小近大機率密度。當然其實也可以用其他對稱的函式。針對每一個觀察中出現的數擬合出多個機率密度分布函式之後,取平均。如果某些數是比較重要,某 些數反之,則可以取加權平均。存在的問題
這種方法會存在一個問題。邊界問題。比如滿足[0,1]之間的均勻分布的數有1000w個,人工大致已經可以看出機率分布。但用核密度估計估計出來的結果會非常奇怪。[-1,0]和[1,2]之間的數的機率密度不會被估計為0。主要原因是因為有邊界的影響。
