定理
 本原元定理
本原元定理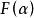 本原元定理
本原元定理 本原元定理
本原元定理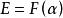 本原元定理
本原元定理在數學中,本原元定理深刻刻畫了什麼時候對於一個域擴張 ,E可以表示為 的形式,即E可以由單個元素生成。一個有限擴張 有本原元,即存在α使得 ,若且唯若 E和 F之間只有有限箇中間域。
證明
如果F是有限域,由於E/F是有限擴張,推得E也是有限域。但是由於有限域的乘法群是循環群,任取這個乘法群的一個生成元,E可以由這個生成元生成。所以在F是有限域的情況下,定理左右兩邊恆為真。
 本原元定理
本原元定理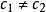 本原元定理
本原元定理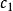 本原元定理
本原元定理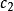 本原元定理
本原元定理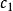 本原元定理
本原元定理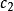 本原元定理
本原元定理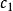 本原元定理
本原元定理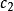 本原元定理
本原元定理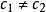 本原元定理
本原元定理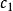 本原元定理
本原元定理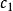 本原元定理
本原元定理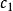 本原元定理
本原元定理如果F是無限域,但是只有有限箇中間域。 先證明一個引理:假設E=F(α,β)並且E和F之間只有有限箇中間域,那么存在一個γ∈E使得E=F(γ)。引理的證明如下:當c取遍F的時候,對於每一個c可以做一個中間域F(α+cβ)。但是由假設,只有有限箇中間域,因此必定存在 ∈F, 使得F(α+ β)=F(α+ β)。由於α+ β,α+ β都在這個域裡,推得( - )β也在這個域裡。由於 ,推得β在這個域裡,於是α也在這個域裡,因此E=F(α,β)是F(α+ β)的子集,F(α+ β)是F(α,β)的子集,於是E=F(α+ β)。引理證畢。
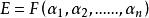 本原元定理
本原元定理 本原元定理
本原元定理由於有限擴張總是有限生成的,推得 (對於 )。利用歸納法以及引理可以得出,如果E/F之間只有有限箇中間域,那么E可以由單個元素生成。
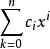 本原元定理
本原元定理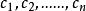 本原元定理
本原元定理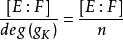 本原元定理
本原元定理而如果E=F(α),假設f(x)=irr(α,F,x)是α在F上的極小多項式,K是任意一個中間域,g(x)=irr(α,K,x)是α在K上的極小多項式。顯然g(x)整除f(x),由於域上的多項式環是唯一分解環,f(x)只有有限個因子。而對於每一個g(x)整除f(x),如果g(x)寫作g(x)= ,並令K=F( )。顯然K是K的一個子域,因此g(x)在K上依然是不可約的。而同時E=F(α)=K(α)=K(α),因此可以得到[E:K]=[E:K]= ,這樣立即推K=K,於是任何一個中間域K對應唯一的一個f(x)的因子g。於是中間域個數小於因子的個數。但因子個數是有限的,因此中間域個數有限。
證畢。
推論
由於有限可分擴張只有有限箇中間域,由本原元定理立刻推出這個擴張有單個生成元。
示例
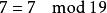 本原元定理
本原元定理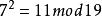 本原元定理
本原元定理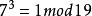 本原元定理
本原元定理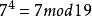 本原元定理
本原元定理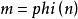 本原元定理
本原元定理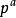 本原元定理
本原元定理 本原元定理
本原元定理模19下7的階為3(
,,,....)模n下a的階,a就是n的本原元,如3是19的本原元,本原元並不唯一(19本原元還有2,3,10,13,14,15),不是所有的整數都有本原元,應是這樣的形式:2,3,,(p為奇素數) 。

